INTRODUCTION

Recently, the scope of the practical use of Benford’s law (Benford 1938) has significantly expanded. Known for over a hundred years, Benford’s law refers to the probability of occurrence of a certain first significant digit in the distribution of various real life data. Contrary to the common assumption that the frequency of occurrence of any first significant digit should be equal, the digit 1 occurs more likely for many data sets! According to Benford’s law, in the decimal system, probability of occurrence of the digit d as the first significant

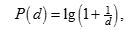                                                                                                                                (1)

accordingly,the probability of  shouldbe , the probability of  d = 2 – 0.18 , etc.

An exhaustive explanation of Benford’s law, covering all cases of its manifestation, has not yet been proposed, although some conditions favouring its emergence are stated. A classic experiment by Benford, showing a good agreement with (1) – analysis of the occurrence of numerals contained in articles of a randomly selected issue of a magazine – is naturally explained by the theorem (Hill 1995), according to which, if one repeatedly randomly chooses a probability distribution and then randomly chooses a number according to that distribution, the resulting data set will obey Benford’s law.

Incomplete understanding does not preclude the successful use of Benford’s law to detecting fraud in accounting and auditing data (Nigrini 2012) andelection fraud(Roukemaa 2014);the applications suggestedextendfrom physics and astronomy (Biau 2015; Hill, Fox, 2016) through seismology(Sambridge et al. 2011)tosteganography(Andriotis et al. 2013) and scientometrics (Alves et al. 2014).

Zenkov (2015) has shown the efficacy of counting frequencies of different first significant digits of numerals for text attribution. It was found that not only for the random combination of texts, but also for the coherent text to which the conditions of the afore-named theorem are not applicable, frequency distribution is close to Benford’s law (1), but the quota of digit 1 considerably exceeds 30 per cent – at least since the word «one» formally being a numeral can actually play the role of an indefinite article. In contrast to the traditional methodology of application of Benford’s law, which treats deviations from the law as an indication of the possible existence of «falsification» (broadly defined), he placed emphasis on the comparison of these deviations for texts by different authors, showing that these deviations are statistically robust author features that allow to distinguish between texts by different authors (under certain conditions, the most important of which is a sufficiently large text).

Basing on these ideas, we present here new research results concerning the distribution of the first significant digits of numerals found in coherent texts.

The study is experimental. The aim of the theoretical substantiation of the results (if such is possible) is not intended which, however, does not diminish the possibility of the practical use of the proposed methodology for practical problems of textual criticism.

For all (Russian-language) texts subjected to computer-aided statistical analysis, we have studied the frequency of occurrence of various first significant digits, taking into account the cardinal as well as ordinal numbers expressed both in figures, and (considerably more often) verbally. In the last case, the first step was to rewrite every form of a numeral with figures (e.g., ‘тысячи четырёхсот пятидесяти трёх’ replaced by ‘1453’) and then to take into account the first significant digit (1) only. To identify the author’s use of numerals, we previously deleted from the text all idiomatic expressions and set phrases accidentally containing numerals («семь пятниц на неделе», «в двух словах»).

Recognition of texts authorship

Authorship of the «Novel with Cocaine»

For sixty years, the Russian literary studies were facing the unresolved problem of authorship of the “Роман с кокаином” («Novel with Cocaine»), published in 1934 under the pseudonym «M. Ageyev». In the absence of reliable information about the author and any other relevant publications under this name the hypothesis has spread about the literary hoax. By virtue of a certain genre and stylistic proximity of the «Novel with Cocaine» to early novels by V. Nabokov, Ageyev’s novel was ascribed to him. Publication of previously unknown archival material in the 1990s (Sorokina, Superfin 1994) refuted this hypothesis. Although this particular philological question has already been solved, we will show the results of applying Benfordian methodology.

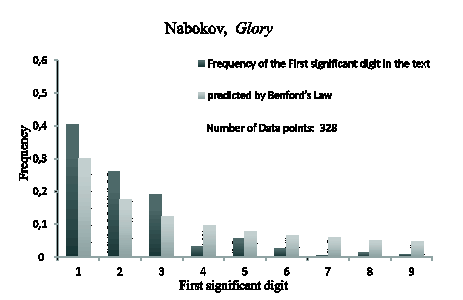
Below are the results of the statistical study of the «Novel with Cocaine» (Fig. 1), and Nabokov’s Russian-language works (Fig. 2, 3 show the results for two novels as an example). Note a dramatic difference in the occurrence of significant digit 1 in Ageyev’s novel, on the one hand, and in Nabokov’s novels, on the other hand. In view of the length of the texts analyzed, this difference can hardly be explained by random fluctuations (unlike subsequent significant digits, which even in the books by the same author behave differently). It is a difference characteristic of the author’s style. We tend to associate it with the psychological peculiarities that, regardless of the will and intention of the author, influence his texts. As for Ageyev, for the reason stated above, the material for comparison is missing, but all works of the first (Russian-language) period of Nabokov’s artistic creation have a similar occurrence of unit as the first significant digit.

Of course, the comparison of the distributions cannot be based merely on the detection of their subjective visual similarities and differences. We have applied the non-parametric Mann-Whitney U test. The null hypothesis, which asserts the absence of significant differences in the distributions considered, was rejected and accepted exactly in the cases, as described above. The difference between Nabokov’s novels turned out to be insignificant, whereas Ageyev’s «Novel with Cocaine» significantly differs from each of them.

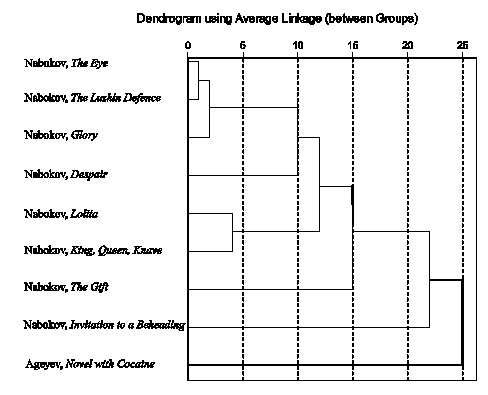
These conclusions are supported by a dendrogram, visualizing the results of the hierarchical cluster analysis. We have analyzed the frequency distributions of the first significant digits of numerals in texts in terms of the similarities/differences between these distributions. Hereinafter, for clustering, the method of average linkage between groups (Gan et al. 2007) (as a balanced approach, avoiding the extremes of the nearest and furthest neighbors methods) with the Chebyshev metric that determines the distance ρ between the n-dimensional numeric vectors x and y as the maximum of the components difference modulus: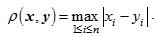. Here, the vector components are frequencies of the first significant digits in each of the texts analyzed. Obviously, the maximum of the difference modulus can be achieved at the i value (i=1,2,…9)  for which the frequencies are originally not small, and this is usually significant digits 1, 2, and 3. However, it is the frequencies of these digits (especially, digit 1) which determine the text specificity in our methodology; that is why we chose the Chebyshev metric.

We have performed the clustering for the «Novel with Cocaine» and almost all of Nabokov’s novels, written in Russian or with the author’s translation into Russian («Соглядатай», «Защита Лужина», «Подвиг», «Отчаянье», «Лолита», «Король, дама, валет», « Дар», «Приглашение на казнь») (Fig. 4). The distance ρ is measured on the horizontal scale; the bigger it is, the less similar the analyzed objects (texts) are. Ageyev’s novel stands out among all the processed texts, joining them at the final stage of clustering.

Thus, the statistical method based on the calculation of the first significant digits of numerals, is able to answer the question about the text authorship.

The problem of «Quiet Flows the Don»

Another well-known problem of texts attribution is the question of authorship of the novel «And Quiet Flows the Don» («Тихий Дон») and, more broadly, the entire literary heritage of M. Sholokhov. There are strong arguments in favor of the plagiarism version, and some arguments against it. The novel consists of eight parts, combined into four books. Linguistic and statistical study of the novel has led many researchers to the conclusion that the text is extremely heterogeneous. The first parts (or at least their Urtext used by Sholokhov) are attributed by many experts to the writer F. Kryukov, although there is another candidate – V. Krasnushkin, and in the text of subsequent parts one discerns the style of A. Serafimovich, B. Pilnyak, A. Fadeev (non-exhaustive list). The opinion has been expressed, that not only the authorship of «Quiet Flows the Don» is doubtful; that also «Virgin Soil Upturned» («Поднятая целина») and «They Fought for their Country» («Они сражались за Родину») are written not by Sholokhov, but by others (in particular, A. Platonov was named) (Kuznetsov 2003).

Without going into detail in the review of the problem, we present our results of the exploration in the framework of Benford’s methodology.

First, we performed a statistical analysis of three novels by Sholokhov (Fig. 5). The distribution of first significant digits of numerals is very different in them, despite the fact that this distribution is usually characteristic of the author.

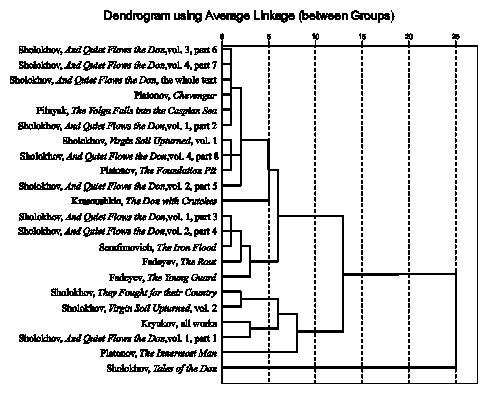
This result made necessary a more detailed comparative analysis of the major works attributed to Sholokhov, as well as texts of some authors, who are considered the true creators of these works: Platonov, “Chevengur” («Чевенгур»), “The Foundation Pit” («Котлован»), “The Innermost man” («Сокровенный человек»); Pilnyak, “The Volga Falls into the Caspian Sea” («Волга впадает в Каспийское море»); Krasnushkin, “The Don with Crutches” («Дон на костылях»); Serafimovich, “The Iron Flood” («Железный поток»); Fadeyev, “The Rout” («Разгром»), “The Young Guard” («Молодая гвардия»). Besides three main novels by Sholokhov, we also analyzed the whole text of his early “Tales of the Don” («Донские рассказы»). The dendrogram of clustering the distributions of first significant digits of numerals is shown in Fig. 6. Some conclusions (confirmed by Mann-Whitney U test):

1) Different parts of «Quiet Flows the Don» and «Virgin Soil Upturned» are distributed across different clusters, which indicates the internal statistical heterogeneity of texts in terms of the distribution of first significant digits of numerals (cf. statistically close «The Rout» and «The Young Guard» by Fadeyev);

2) The assumption that Platonov, Pilnyak, and Serafimovich could participate in the creation of the text of «Quiet Flows the Don» and the first book of «Virgin Soil Upturned», is not ungrounded;

3) Authorship of Krasnushkin in regard to the «Quiet Flows the Don» is more doubtful;

4) «They Fought for their Country» and the second book of «Virgin Soil Upturned», chronologically created in the same era may pertain to the same author;

5) Kryukov’s texts are statistically close to the initial parts of the «Quiet Flows the Don».

6) It is highly doubtful that «Tales of the Don «, on the one hand, and «The Quiet Don», «Virgin Soil Upturned», «They Fought for their Country» belong to the same author.

These findings are in good agreement with the results briefly described above which were obtained by other (mainly, philological) methods.

Note that (all available for analysis) Kryukov’s texts are relatively small in size, so we had to merge them into one file for statistical analysis. The same applies to Sholokhov’s «Tales of the Don». Available for analysis was only one text by Krasnushkin. Platonov’s «The Innermost Man» is relatively small, which could affect the statistical significance of the results for this novel.

Thus, Benfordian analysis can be useful in the study of text’s authorship.

Testing of methodology: Nekrasov‘s early prose

An interesting opportunity of testing the idea about the relation of text authorship to its statistical characteristics is provided by the novels «Three Parts of the World» («Три страны света») and «The Dead Lake» («Мертвое озеро») written by N. Nekrasov, much better known as a poet, at the beginning of his literary career, together with A. Panayeva and first published in 1848–1849 and 1851, respectively.

The manuscripts of novels have not been preserved, so the question of the division of labor between the co-authors should take into account their own testimonies. In Panayeva’s «Memoirs» («Воспоминания»), writing «Three Parts of the World» is ascribed to the two – both Nekrasov and her; as for «The Dead Lake», the participation of Nekrasov was limited to the elaboration of the plot and writing a small part of the text. Guided by philological considerations, literary scholars – contrary to Panayeva’s testimony – discern in both novels a substantial part of the text, written by Nekrasov (with indication of specific chapters) (Nekrasov 1965; Nekrasov 1985).

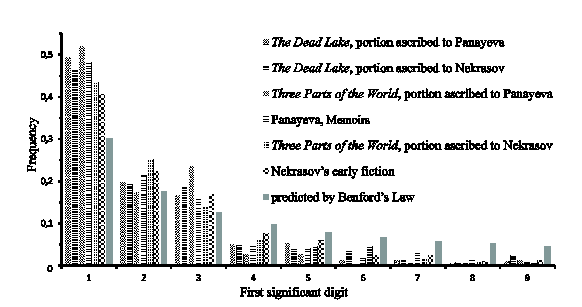
We have counted the frequencies of various first significant digits of numerals in parts of each novels attributed by literary scholars to a specific author (Nekrasov, Panayeva), and, for comparison, performed the same analysis for Panayeva’s «Memoirs», as well as for the early prose works by Nekrasov as the sole author (Fig. 7).

Some conclusions:

1) The distributions of first significant digits of numerals in parts of “The Dead Lake» attributed to Nekrasov and Panayeva are generally similar and comparable with the results for the part of «Three Parts of the World», attributed to Panayeva (except for numbers 3, in which the graph shows outlier). For Panayeva’s «Memoirs», similar results have been obtained.

2) The distribution of first significant digits of the numerals in chapters of «Three Parts of the World», attributed to Nekrasov, significantly differs from the three above mentioned distributions, but is similar to that for Nekrasov’s early fiction. Panayeva’s participation in writing this part of the novel, too, is not excluded.

3) From this, it follows that different parts of “The Dead Lake» are probably written by the same author, namely – Panayeva, but different parts of «Three Parts of the world», indeed, have a different authorship.

4) So, there is no reason not to trust Panayeva in her testimony about the process of writing her two joint novels with Nekrasov.

The text indicated in the figure 7 as Nekrasov’s early fiction incorporates «The Story of a poor Klim» («Повесть о бедном Климе»), «The Life and Adventures of Tikhon Trostnikov» («Жизнь и похождения Тихона Тростникова»), «Surguchov» («Сургучов»), «The Thin Man, his Adventures and Observations» («Тонкий человек, его приключения и наблюдения»), «On the same Day at eleven o’clock…» («В тот же день часов в одиннадцать утра…») (Nekrasov 1984).

We believe that our methodology can be a useful addition to traditional textual practices, taking into account sentence length, word length, occurrence of certain words and parts of speech, etc. (Mitkov 2003; Aronoff, Rees-Miller 2004).

CONCLUSION

1) Benford’s law holds approximately for coherent texts.
2) Deviations from Benford’s law are statistically significant author features that allow, under certain conditions (the most important of which is a sufficient length), to distinguish between the texts with a different authorship.
3) The actual frequency of occurrence is higher than the probability according to Benford’s law for significant digits 1, 2, 3; for the subsequent digits the situation is reversed. At the end of {1, 2,…, 8, 9} row, the digits distribution is characterized by strong fluctuations and thus is unrepresentative for our purpose.