1.Introduction

  Features of the development of cognitive reflection in primary school is one of the important problems of pedagogical psychology. The purpose of this study was to determine the nature of the distribution of types of cognitive reflection in the first and second years of education in elementary school.

The activity approach in the study of cognitive actions suggests that children need to be offered tasks, the condition for the successful completion of which is the child’s cognitive reflection.

Cognitive reflection, associated with the child’s awareness of the way of his actions, involves its consideration [2]. Depending on the purpose for which it is carried out and what is supposed to be established, it is advisable to distinguish between two types of awareness of the mode of action, or two types of reflection as a person’s appeal to his own actions.

Thus, if the consideration of the method of actions is carried out in order to find out what operations must be performed and what must be done concretely in order to obtain the required result, then in this case the child is aware in his actions only of their visual characteristics.

This level of consideration of the mode of action is characterized by the awareness of its features given in direct perception, and is a manifestation of formal cognitive reflection, since it reflects the dependence of the mode of action on random and individual conditions for its implementation.

In this case, with the successful solution of problems that have an objectively general principle of construction, the child, when oriented to the external similarity of the features of the conditions of the problems, can group them formally, and when oriented to the external difference of these features, he can generally refuse to group, considering the tasks different.

If, however, the consideration of the method of actions is carried out in order to find out why this action is performed in this way and what is in this action the reason for its successful performance under different conditions (when solving different, but related tasks), then the child realizes the method of his actions, relying on his hidden, not directly observable characteristics, and can therefore generalize actions meaningfully. This level of consideration of the method of action is a manifestation of internal or meaningful cognitive reflection, since it reflects the dependence of the method on the necessary and essential conditions.

In this case, with the successful solution of problems that have a common principle of construction, the child, oriented toward the internal, essential unity of these problems, can group them meaningfully. Therefore, the understanding of the proposed tasks as belonging to the same type, which is based on a generalization of the method for solving them, can serve as an indicator of the awareness of the connection of the method with significant relationships, i.e. an indicator of the implementation of meaningful cognitive reflection.

2.Materials and methods

2.1 Characteristics of the experimental situation

To determine the type of reflection in solving problems, a general scheme for constructing an experimental situation was developed [3; 4; 5; 6], the modification of which was used in works on non-educational [7] and educational material [1; 8].

In its first part, the subject was asked to solve several problems, which, firstly, should belong not to one, but to two classes (or subclasses), which means that part of the tasks is solved on the basis of one principle, and part with the use of the other, and, secondly, the conditions of the tasks must differ in external, directly perceived features.

In the second part, in the case of a successful solution of problems, they need to be grouped. By the nature of the grouping, the presence or absence of meaningful, internal reflection was determined in their solution.

If a significant commonality of methods for solving problems was taken as the basis for grouping, then, in the process of solving them, meaningful cognitive reflection was carried out, and if the external similarity of the features of their conditions was taken as the basis, then, consequently, meaningful cognitive reflection, as an understanding of the connection between actions and essential ¬ny relations and generalization on their basis of the method of solution — was absent, — there was a formal reflection.

Thus, the mastery of the initial forms of cognitive reflection is characterized by the child’s ability to meaningfully generalize the method of action in solving problems, i.e. reveal the essential commonality of the methods of their actions when solving problems of the same kind and highlight the fundamental difference between the implemented methods when solving problems of various kinds. In this case, the child relies on the knowledge of the reasons for his actions, on the knowledge of why he acted in this or that way when solving problems.

2.2 General characteristics of the experimental work

To conduct the study, the «Jumping figures» technique was developed. It included three tasks for moving three-dimensional geometric figures made of wood around the game cell field: a cylinder, a cone and a tetrahedral prism according to certain rules. A total of 138 children participated in the study: 38 first graders at the beginning of the school year (October), 49 first graders at the end of the school year (May) and 51 second graders also at the end of the school year (May).

2.2.1.Features of an individual experiment

The experiments were carried out individually as follows. In the first part of the experiment, the child was taught the rules and methods of moving around the cellular playing field of each of the three volumetric geometric figures used in solving problems — a cylinder, a cone and a prism (the children were told that these were new chess pieces).

In the second part of the experiment, the child solved the proposed tasks. In the third part, he answered the question of the experimenter, who said: “You solved three problems. These problems were solved by many children. Some children said that all tasks are similar, others — all tasks are different. Children of another group said that tasks 2 and 3 are similar, but task 1 is different from them. The children of the other group said that tasks 1 and 3 are similar, but task 2 is different from them. Children of the third group said that tasks 1 and 2 are similar, but task 3 is different from them. Who do you think said the right thing?»

2.2.2. Contents of the first part of the experiment

At the very beginning of the first part of the experiment, the child was given a playing cell field of the same size as a chess field: 8 cells horizontally and 8 cells vertically (each cell had the shape of a square with a side of 3 cm, — Fig. 1.

Then they gave him a top hat and said: “This is a new chess piece. She can walk across the cell field directly into the neighboring cell and obliquely. She can also jump. Her jump is equal in length to two different steps in one direction — straight and oblique or oblique and straight ”(Fig. 2, — a, b, c, d).

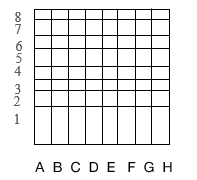
Figure 1. Playing field.

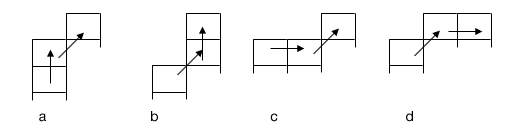
Figure 2. Cylinder displacement

Next, the child tried to walk and jump with a cylinder from different cells of the playing field. At the end of teaching the movements of the cylinder, a control task was proposed, where it was required to show all possible jumps from some central cell of the field, for example, from cell D5 (it should be noted that the names of the cells of the playing field were not mastered by the children).

After the child mastered the steps and jumps of the cylinder, he was asked to learn how to move the cone (Fig. 3). One of his steps was a move obliquely to the next cell (see the second step in option «a», the first step in option «b», the third step in option «c»).

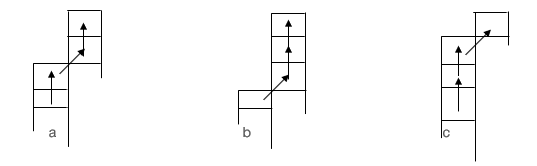
Figure 3. Movement of the cone

The other two steps were related to moving the cone directly to the adjacent cell (see the first and third steps in option «a», the second and third in option «b», the first and second in option «c»).

The child was first shown how the cone was walking and jumping, and then they were asked to make a series of jumps for them. In conclusion, the child was given a control task: one of the central cells of the field was indicated (for example, G4) and asked to perform all possible jumps from this cell with a cone. After the successful completion of this task, he was presented with a prism.

The prism steps into the neighboring cell only obliquely and its jump is equal to three such steps (Fig. 4, — options «a» and «b»).

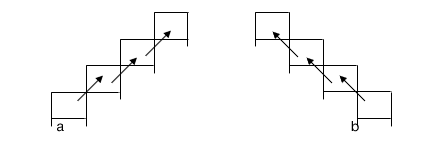
Figure 4. Movement of the prism

The child was first shown how the prism steps and jumps, then they were offered to independently perform individual jumps with it from different cells of the playing field. After everything, the child had to complete the control task — to show all possible jumps of the prism from some central cell of the playing field, for example, from cell D4. The first part of the experiment ended with mastering the prism jumps.

It should be noted that when mastering the methods of moving figures, the children differed in the following characteristics.

Firstly, there were differences in the speed of performing control jumps: someone acted slowly, someone quickly.

Secondly, there were differences in the form of jumps: some children jumped in a straight line from the initial cell of the jump to the last cell found (see Fig. 5); others “jumped” differently: they repeated the contour of the movement of this figure in steps (see Fig. 2 and 3).

Thirdly, there were differences in the number of cells included in the circuit of the jump: some of the children, moving the figures, counted the cells aloud, others counted the cells not in terms of external speech (not aloud), but in terms of internal speech (silently, “to themselves”) , — this could be judged by the characteristic nods of the head; in a third of the children, there was no cell counting at all (both in terms of external and internal speech).

Fourthly, there were procedural differences in the movement of figures when performing jumps: a number of children moved figures directly across the playing field, a number of children transferred figures over the playing field from the initial cell of the jump to the final one.

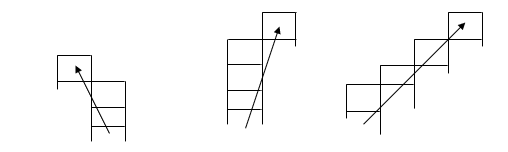
Figure 5. Jump “in a straight line”

An analysis of the experimental protocols showed certain connections between the noted features of the movements of the figures in the control tasks.

The children who acted without errors were characterized by the following: they acted relatively quickly, made jumps in a straight line from the given initial cell of the jump to the last cell found, did not count the cells included in the circuit of the jump, neither in terms of external speech, nor in terms of inner speech. , the pieces above the playing field were transferred (rather than moved on the surface of the playing field).

The children who made few mistakes in the control tasks acted at different speeds: the majority acted quickly, while the minority acted slowly. At the same time, both children jumped in a straight line from the given initial cell of the jump to the last cell found, counted the cells in terms of inner speech, and transferred the figures over the playing field (and did not move them along the surface of the playing field).

The children, who made many mistakes in the control tasks, acted slowly, made jumps, repeating the contour of the movement of the given figure with steps, and moved the figures along the surface of the playing field.

Consideration of the noted differences in the assimilation of movements of figures by children of different ages showed that by the end of training in the second grade, the number of children in the three groups noted had changed.

So, the number of children — performing jumps slowly, reproducing the contour of the steps of the figure; moving pieces touching the playing field; those who counted the cells of the playing field in terms of inner speech and, especially, in terms of external speech, both simultaneously with the movement of the figure, and before its movement; figures performing jumps with a small number of errors and, especially, with a large number, decreased.

And the number of children who jumped relatively quickly, in a straight line, in the absence of cell counting (in terms of external and internal speech) and without the figure touching the playing field, increased.

The number of children who acted without errors or with a small number of errors also increased, and the number of children who made many mistakes when performing control tasks to assess the degree of assimilation of jumps of the three proposed figures decreased: cylinder, cone and prism.

2.2.3 Content of the second part of the experiment

In the second part of the experiment, the children solved three problems.

In the first problem, it was necessary to get from cell B3 to G3 by two jumps of the cylinder. To do this, the experimenter placed a cylinder in cell B3, and a cardboard circle in cell G3 (Fig. 6).

After successfully solving the first problem (independently or with help), it was proposed to solve the second problem, where you need to make two jumps with a cone. To do this, the experimenter placed the cone in cell B2, and the cardboard circle—its location indicated the point where the cone should land after two jumps from cell B2—was placed in cell D8 (Fig. 7).

After successfully solving the second problem (on their own or with help), the child was asked to solve the third problem, in which it was required to make two jumps with a prism. To do this, it was placed in cell A4, and the cardboard circle was placed in cell G4 (Fig. 8).

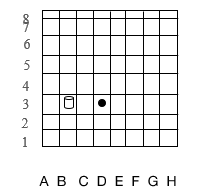
Figure 6. Problem for jumping a cylinder

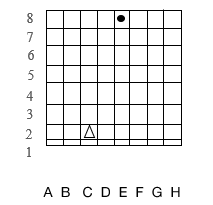
Figure 7. Problem for cone jumps

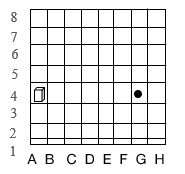
Figure 8. Prism jumping problem

According to the peculiarities of solving problems, the children differed as follows.

First, there were differences in orienting actions in solving problems. Some children had an independent preparatory stage before performing both required actions for solving problems, within the framework of which a general orientation (with the help of perceptual actions) was carried out in the content of the proposed task.

Other children did not have such a stage of general orientation in the task: they deployed orientation in the content of the task before performing each of the two jumps: it is true that orientation was carried out more often before the first jump than before the second.

It is important to note that one part of the children in this group searched for the first move only in the first task for a long time, another part only in the second task, and a third part in the first and second tasks.

Secondly, there were differences in the independence of problem solving. In some cases, the children were able to figure out their mistakes on their own (without the help of the experimenter) and solve problems correctly. In other cases, the children were able to solve the problem only with the help of the experimenter, since they could not find the first jump on their own. At the same time, one part of the children needed help in solving only the first problem, another part — in solving only the second problem, and a third part — in solving the first and second problems.

Thirdly, similarly to the actions at the previous stage of the experiment (on mastering the rules for moving figures), there were differences in the shape of the jumps of the figures: one child made both jumps of the figures in a straight line, first from the given initial cell of both jumps to the found last cell of the first jump, then from the found last cell of the first hop to the given last cell of the second hop; other children made both jumps, repeating the contour of the movement of this figure with steps.

Fourthly, just as when learning the rules for moving pieces, there were procedural differences in the performance of jumps: some children moved pieces directly across the playing field, others performed jumps, transferring figures over the playing field from the initial cell of the first jump to its final cell and from this cell to the end cell of the second jump.

An analysis of the experimental protocols, which reflected the noted characteristics of problem solving, showed certain relationships between these characteristics and the success of problem solving.

Children who have successfully solved problems are characterized by independence of behavior, as well as the presence of orienting actions: either in relation to the entire problem (before performing both jumps), or in relation to each of the two jumps separately. At the same time, they made both jumps in a straight line: first, from the given initial cell of both jumps to the found last cell of the first jump, then from the found last cell of the first jump to the given last cell of the second jump. At the same time, none of the children who successfully solved all the problems touched the surface of the playing field when moving the pieces.

Children who solved the problems unsuccessfully needed the help of the experimenter, which usually consisted of hints for the correct first jump, either when only the first problem was solved incorrectly, or when only the second problem was incorrectly solved, or when both of these problems were solved incorrectly. At the same time, it is typical for the children of this group to perform both jumps with a detailed reproduction of the contour of the steps of the corresponding figure and the movement of the figures along the surface of the playing field.

An analysis of the protocols for solving problems by students in the first and second grades revealed that by the end of training in the second grade, the number of students who solved problems on their own increases, and the number of students who need the help of an experimenter when solving problems decreases.

The second part of the experiment ended with the solution of the third problem.

2.2.4 Content of the third part of the experiment

In the last, third part of the experiment, as mentioned above, the child was asked to evaluate 5 opinions about the tasks, thereby expressing his own: «… all tasks are similar …», «… all tasks are different …», «…the first task is different from the other two…», «…the second task is different from the other two…», «…the third task is different from the other two…».

Based on the ideas outlined above about the two types of cognitive reflection, the child’s opinion about tasks was interpreted as a reflection of the nature of understanding their subject content.

If the child believed that all tasks are similar, pointing out such features of their conditions, for example: in all tasks it is required to find two jumps, all tasks are related to moving pieces around the playing field, in all tasks after two jumps you need to get into the cell , where there is a cardboard circle, etc., then in these (and similar) cases it was assumed that the child solved problems on the basis of a situational understanding of their subject content, since he judged problems based only on external features their conditions (opinion No. 1).

If the child believed that all tasks are different, pointing out such features of their conditions: in all tasks different three-dimensional geometric figures are used, all figures walk and jump in different ways, etc., then in these (and cases similar to them) (as in the previous case), it was assumed that the child solved problems on the basis of a situational understanding of their subject content, since he judged problems by the external features of their conditions: the characteristics of the movements of the figures, their visible differences, the location jumping places on the playing field (opinion No. 2).

Along with the children who considered the tasks different or similar (for various reasons given above), there were children who believed that among the proposed tasks there was one that did not fit the other two.

One part of the children in the group under discussion believed that the first task did not fit the other two, because «… in it the figure jumps close …», and in the second and third tasks «… the figures jump far …» (opinion No. 3).

Another part of the children of this group believed that the third task did not fit the other two, because «… in it the figure jumps straight …», and in the first and second tasks «… the figures jump with a turn …» (opinion No. 5).

Qualifying the opinions of these groups of children, it should be said that they reflect the diversity of situational understanding by children of the subject content of the tasks they solved. So, pointing out the difference between the third task and the first two or the first task from the second and third, the children are actually guided by the external features of the conditions of the tasks that they knew before solving the problems (at the stage of mastering the ways of moving figures), in particular, on the features jumping figures. Such an understanding indicates the implementation of formal reflection in solving problems on the movement of three-dimensional geometric figures.

Some of the children participating in the experiments pointed out the difference between the second task and the first and third. These children believed that the second task was not suitable, because the movement of the figure in it had a different form. In particular, the children noted that in the second task all the jumps “…are made along the same line…, go in the same direction…”, and in the first and third tasks the figures “…go straight and backward…, forward and backward…”. In this case, it was assumed that the children meaningfully generalized the ways of solving the first and third tasks, highlighting the internal relationship of these tasks (opinion No. 4).

The validity of such an opinion of children about tasks corresponds to our plan when constructing these tasks: the first and third tasks are referred to as the so-called “mirror” tasks, since in them the second jump is, as it were, a mirror (symmetrical) reflection of the first jump. In the second problem, however, there is no such symmetry between the two jumps: the second jump is a continuation of the first in the same direction.

Thus, based on the understanding of the characteristics of formal and meaningful cognitive reflection, it can be argued that the children of this group carried out meaningful cognitive reflection when solving problems.

3.Results

The distribution of subjects who expressed different opinions about the solved tasks is No. 1 (all tasks are similar), No. 2 (all tasks are different), No. 3 (the first task differs from the other two), No. 4 (the second task differs from the other two others), No. 5 (the third task differs from the other two), is presented in the table.

Table

The number of children in the 1st grade (October and May) and in the 2nd grade (May) who expressed opinions No. 1, No. 2, No. 3, No. 4 and No. 5 on the tasks — (in %).

The data presented in the table reflect the features of the distribution of types of cognitive reflection in the first and second grades of elementary school.

First, it should be noted that as they study in the first half of elementary school, the number of children who carried out meaningful cognitive reflection in solving problems increases: by the end of the first grade — by 7.9% (from 10.5% in October to 18.4 % in May), by the end of the second grade — by 9.0% (from 18.4% to 27.4%).

Second, there are changes in the distribution of children who have carried out formal cognitive reflection in solving problems.

On the one hand, the number of children who considered all tasks similar (opinion no. 1) and all tasks different (opinion no. 2) decreased. During the first grade, the decrease in these groups of children was, respectively, 12.5% ​​(from 42.1% to 30.6%) and 5.6% (from 34.2% to 28.6%). During the second grade, the decrease was, respectively: 11.0% (from 30.6% to 19.6%) and 5.1% (from 28.6% to 23.5%).

On the other hand, there was an increase in the number of children who believed that the first problem did not fit the other two and that the third problem did not fit the others. During the first grade, the increase in these groups of children was, respectively, 4.9% (from 5.3% to 10.2%) and 4.3% (from 7.9% to 12.2%). During the second grade, the increase was, respectively: 5.5% (from 10.2% to 15.7%) and 1.6% (from 12.2% to 13.8%).

Thus, the analysis of the data in the table under consideration makes it possible to outline some trends in the dynamics of the distribution of types of cognitive reflection over the course of two years of education in elementary school.

The first trend is associated with an increase in the number of children who carry out meaningful reflection when solving problems.

The second trend is associated with a multidirectional change in the number of children who carry out formal cognitive reflection: the number of children who give a common, undifferentiated characteristic of three tasks (“everyone is similar” or “everyone is different”) decreases, and the number of children who give a differentiated description of tasks (one task does not fit to the other two) increases.

4.Conclusion

So, a study was conducted aimed at determining the characteristics of the age-related dynamics of cognitive reflection in the first half of education in elementary school (first — second grades).

The results obtained indicate that the noted age dynamics is characterized by a redistribution of the number of children who express different opinions about the solved problems. Thus, the number of children with undifferentiated formal reflection decreases (these children consider all solved problems to be either similar or different) and the number of children with differentiated formal reflection increases (these children believe that among the solved problems either the first problem does not fit the other two, or the third ).

And, most importantly, during the time of study in the first and second grades, the number of children with meaningful cognitive reflection, highlighting the essential unity of the first and third tasks, increases.

In further research, it is planned to determine the characteristics of the age-related dynamics of cognitive reflection in the second half of primary school education (third-fourth grades).