1.Introduction.
Thinking, as is known, has three main forms of implementation: visual-active, visual-figurative and verbal-discursive [3].
In younger schoolchildren, — thanks to school education, associated, in particular, with solving typical problems in mathematics, — the nature of thinking (in comparison with preschoolers) changes: the child can now highlight essential connections and relationships in objects, i.e. carry out substantive analysis when solving problems.
When mastering substantive planning, younger schoolchildren begin to point out essential connections not only when operating with real things, but also when operating with their images.
Thanks to the development of substantive reflection, children master verbal-discursive thinking activity and, relying on the foundations of their activity, have the opportunity to operate in a generalized way to solve outwardly different problems.
The implementation of content analysis, content planning and content reflection indicates the implementation of theoretical type thinking by children, which is fundamentally different from empirical thinking, since it is based on the implementation of formal analysis, in which essential and non-essential connections are not distinguished, — (for more details on the implementation of content levels of analysis, planning and reflection as components of theoretical thinking when solving problems, see the work of V.V. Davydov [ 1 ]).
The work in question was aimed at identifying the features of mastering theoretical type thinking activity by primary school students — studying according to the experimental programs of D.B. Elkonin and V.V. Davydov [ 1 ] and regular primary school programs,
- Materials and methods
The stated goal involved the implementation of 3 experimental series reflecting 3 plans for the implementation of thinking activity when solving problems: subject plan, figurative and discursive.
2.1. The first experimental series.
Here, a technique conventionally called «Letter-digital correspondences» [ 2 ] was used. The experiments were conducted individually. First, the student was asked to solve 2 training problems, using which he learned the rules for moving cards. Then, using the learned rule for rearranging cards, the student was asked to solve six main problems in which the number of letters and numbers increased.
Training problems
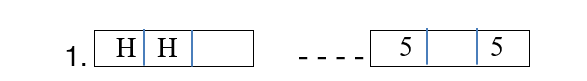
To solve this problem, you need to arrange the cards that have a letter in the same way as the cards that have a number. One rearrangement of a card to an empty space is the execution of one action.
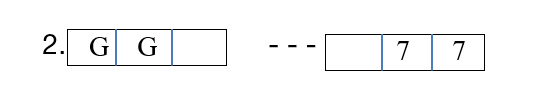
In this problem, you also need to arrange the cards that have a letter in the same way as the cards that have a number by performing one rearrangement.
Main tasks
- In 3 permutations, arrange cards with identical letters (C) (C) (T) ( ) in the same way as cards with identical numbers ( ) (3) (1) (1).
- In 3 permutations, arrange ( ) (R) (M) (M), as (2) (2) (4) ( ).
- In 3 permutations, arrange (B) (B) (B) (V) ( ) – ( ) (6) (7) (7) (7).
- In 3 permutations, arrange ( ) (N) (D) (D) (D) – (5) (5) (5) (6 ) ( ).
- In 3 permutations, arrange (G) (G) (G) (G) (L) ( ) – ( ) (5) (8) (8) (8) (8).
- Arrange in 3 permutations ( ) (B) (F) (F) (F) (F) – (1) (1) (1) (1) (7) ( ).
The main tasks are of the same type, since they are developed on the basis of a single algorithm: among a row of letters and a row of numbers there are unique and repeating signs, in any row a free cell among the letters is placed where the repeating digit is, and a free cell among the numbers is placed where the repeating letter is.
A general approach to the six main tasks is possible on this principle: in any task, the 1st permutation involves moving a card placed in the place of a unique digit to a free cell, the 2nd permutation requires that the card with a unique letter get into the free cell; the 3rd permutation is associated with moving a card located in the location of numbers where the free cell is to the free cell.
2.1.1. Results.
Data on the number of first-graders, second-graders, and third-graders who use a generalized, theoretical method to achieve the required result in problems with letters and numbers when mastering the content of experimental and standard programs are contained in the first table.
Table 1
The number of first-graders, second-graders, and third-graders studying according to experimental and standard programs who solved problems based on a generalized approach.
| Classes
|
Educational programs | |
| Experimental | Regular | |
|
First
|
27 (48,2%) |
14 (25,9%) |
|
Second
|
34 (66,7%) |
28 (52,8%) |
|
Third
|
46 (83,6%)
|
37 (71,2%)
|
Based on the consideration of the presented data, it is possible to identify features that characterize the formation of theoretical thinking in children who studied according to different programs.
When mastering the standard program, children with a generalized approach to problem solving are distributed among classes as follows: after the end of the first grade, these children made up a quarter of the contingent, after two years — one half, after three years — a little more than two thirds.
When studying according to experimental programs, children who solved problems in the indicated way made up: after the first year, about one half, after two years – two thirds, after three years – a little more than four fifths.
Comparing the dynamics of the development of thinking in children when studying according to different programs, we can highlight some differences. Thus, when studying according to the experimental program, the greatest increase in the number of «theorists» in one academic year occurs in the first grade, and when studying according to the standard program — in the second grade. In the first situation, the number of «theorists» increased by 31.4% (i.e., approximately by 1/3), in the second situation — by 28.3%.
Moreover, the number of students using the generalized method at the end of the first grade in experimental programs is almost equal to the number of students who have mastered the content of regular programs for two years.
A similar picture is observed among schoolchildren using the theoretical method at the end of the 2nd and 3rd grades, when mastering the content of experimental and conventional programs, respectively: 66.7% and 71.2% (the difference is only 4.5%).
Consideration of the contents of Table 1 leads to the following statement: when mastering the content of conventional programs, approximately the same number of «theoreticians» are reproduced with a delay of one year as when mastering the content of experimental programs.
2.2. The second series of experiments.
In the second series of our experimental work, the features of the transition of younger schoolchildren from empirical to theoretical thinking when solving problems in a visual-figurative form were clarified. A technique called «Moving a Chess Piece» was developed. It included eight problems, the solution of which required mental (internal) manipulation of an imaginary object called a «chess knight», since its mental movement had to be carried out according to the rules of the move of this piece.
The experiment was conducted frontally. First, the experimenter drew a playing field on the board (Fig. 1) and then explained to the children the names of its cells, consisting of a combination of a letter and a number.
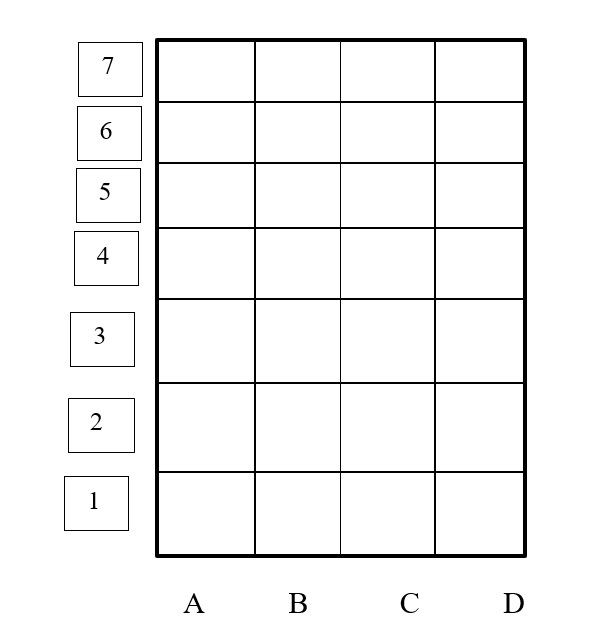
Fig. 1. Playing field.
The children learned the moves of a chess knight: the experimenter explained how the knight moves in two moves and how these moves are recorded. Each child received a form with eight problems.
FORM
Training problems
- Which cells can a knight get to in one move from cell B7.
- Which cells can a knight get to in one move from cell B1.
Main problems
- A7 — ? — B7
- A6 — ? — B6
- A5 — ? — B5
- A7 — ? — ? — G5
- A6 — ? — ? — G4
- A5 — ? — ? — G3
The experimenter checked the solution of the training problems with each student and corrected the mistakes, and the children solved the main problems independently. They were explained that in the first, second and third problems it is necessary to find two movements of the knight, and in the fourth, fifth and sixth problems it is necessary to find three movements of the knight.
All the main problems belong to one class, since they have a single principle of construction, according to which, with the correct solution, the knight can only move vertically. In accordance with this principle, the general method of solving all the main problems assumes that the first movement of the knight should be only on vertical B, and not on vertical C. The last movement of the knight is quite possible according to the rules. But in this case, it is impossible to solve the problems in two and three movements.
If the children managed to solve all six main problems correctly, then we considered that the subjects acted in a generalized, theoretical way, revealing the general principle of the solution. If the children did not solve all the problems (for example, did not solve the fourth, fifth and sixth problems) or some problems were solved incorrectly, then we assumed that in this case the students acted in a non-generalized, empirical way, when each problem was considered separately (as not related to the other problems) and solved, accordingly, as an independent one.
2.2.1. Results.
The distribution of children studying in the first, second and third grades according to experimental and regular primary school programs and solving problems of the «Moving a Chess Piece» method in a general, theoretical way is presented in Table 2.
Table 2
The number of schoolchildren in the first, second and third grades studying according to experimental and regular programs, using a theoretical method in solving problems.
| Classes
|
Educational programs | |
| Experimental | Regular | |
|
First
|
23 (40,4%) |
18 (31,0%) |
|
Second
|
32 (61,5%) |
24 (43,6%) |
|
Third |
43 (74,1%)
|
32 (62,5%)
|
An analysis of the data in Table 2 allows us to identify a number of points characterizing the development of theoretical thinking in primary school students who studied according to different programs, associated with the development of a general method of solving problems in a visual-figurative form.
Thus, the greatest increase in the number of «theorists» in the experimental classes occurs in the second year of study (21.1%), and in a regular school — in the third year of study (16.0%).
As in the analysis of the data obtained in individual experiments of the first study (where children solved problems in a visual-active form), attention is drawn to the fact that the number of «theorists» in the experimental classes after the first and second years of study is approximately equal to the number of «theorists» in regular classes after two and three years of study.
In general, the results of the second series of experiments (as well as the above-mentioned results of the first series) indicate that teaching primary school students according to the experimental program creates more opportunities for the implementation of the theoretical method of solving problems in a visual-figurative form — children move on to theoretical thinking earlier when solving problems in a visual-figurative form (on non-educational material) than their peers studying according to regular primary school programs.
2.3. The third series of experiments.
In the third series of our experimental work, the features of the transition of primary school students from empirical thinking to theoretical thinking when solving problems in a verbal-discursive form were clarified. A technique called «Who is older? Who is younger?» was developed. This technique is designed to identify the features of thinking of primary school students when solving plot-logical problems.
The experiment was conducted in a group form. Children were asked to solve ten problems in which it was necessary to draw a conclusion based on the correlation of judgments proposed in their conditions.
FORM
- In 5 years, Borya will be the same age as Masha is now. Who is younger?
- In 6 years, Dima will be the same age as Sveta is now. Who is older?
- In 5 years, Kolya will be 3 years older than Ira is now. Who is younger?
- In 8 years, Borya will be 4 years older than Dima is now. Who is older?
- In 6 years, Nina will be 9 years older than Rita is now. Who is younger?
- In 3 years, Marina will be 6 years older than Galya is now. Who is older?
- In 17 years, Vova will be 12 years younger than Ira is now. Who is younger?
- In 16 years, Vanya will be 14 years younger than Slava is now. Who is older?
- In 13 years, Alik will be 19 years younger than Vanya is now. Who is younger?
- In 11 years, Sasha will be 15 years younger than Nina is now. Who is older?
The first two problems are introductory, relatively simple, they orient children in the reality that is associated with comparing age indicators in the present and future tenses.
The remaining eight problems belong to the same class, since they have a single principle of construction, which is based on the ratio of the ages of both characters presented in the conditions of the problems.
The general method of solving problems is based on this principle: if the number of years — in which one of the characters will be older – is greater than the number of years by which he will become older, then this participant is younger than the other.
As in the two previous series, the experiment was conducted in the third quarter of the school year with first, second and third grade students studying according to experimental and regular primary school programs.
After distributing the forms with the problems, the experimenter answered the children’s questions related to the content of the first two problems, and starting with the third problem, the children solved them independently.
A series of eight main problems (from the third to the tenth) was constructed in such a way that all the problems differed in the external features of the conditions: in the odd problems the word «younger» was used in the wording of the question, and in the even problems — the word «older».
The conditions of the third, fourth, fifth and sixth problems included single-digit numbers, and the conditions of the seventh, eighth, ninth and tenth problems included double-digit numbers.
In the conditions of the third, fourth and seventh, eighth problems, the same ratio of numbers was presented: the first number encountered in the problem condition was greater than the second. In the conditions of the fifth, sixth, ninth and tenth problems, a different ratio of numbers was presented: the first number encountered in the problem condition was less than the second.
The above circumstances made it possible to ensure, as preliminary individual experiments showed, a significant external, random, insignificant difference in the conditions of the problems.
When processing the data characterizing the results of problem solving, we assumed that the problem solving was carried out in a general, theoretical way if all the problems (or with the exception of one) were solved correctly. If some of the problems or all the problems were solved incorrectly, then in this case it was considered that the student acted in a private, empirical way.
2.3.1. Results.
The distribution of children studying in the first, second and third grades according to the experimental and regular primary school programs and solving the problems of the «Who is older? Who is younger?» methodology in a general, theoretical way is presented in Table 3.
Table 3
The number of schoolchildren in the first, second and third grades studying according to the experimental and regular programs, using the theoretical method in solving problems.
|
Classes
|
Educational programs | |
| Experimental | Regular | |
|
First
|
15 (27,8%) |
11 (19,6%) |
|
Second
|
20 (35,7%) |
16 (27,6%) |
|
Third
|
36 (63,2%)
|
25 (45,5%)
|
The analysis of the data in Table 3 allows us to highlight a number of points characterizing the development of theoretical thinking in primary school students studying according to different programs, associated with the development of a general method for solving problems in verbal-discursive form.
In the results of the third series of experiments, it is noteworthy that during the period of study in the third grade, the increase in the number of «theoreticians» in the experimental classes becomes significantly greater than in regular classes, respectively: 27.5% and 17.9%.
This increase leads to the fact that by the end of primary school the number of «theorists» among students in experimental classes differs significantly from the number of «theorists» among students in regular classes.
Moreover, an even greater difference is found if we compare how the number of «theorists» in experimental classes changes — from the first to the third grade: in the first case, the increase is 35.4%, in the second – 25.9%.
The noted facts indicate that teaching primary school students according to the experimental program to a greater extent contributes to the transition of children from empirical thinking to theoretical thinking when solving problems in verbal-discursive form than teaching according to the regular program.
- Conclusion.
This work was aimed at establishing the number of primary school students who have formed a generalized, theoretical approach to solving various problems of a non-educational nature in subject, figurative and discursive terms.
For this purpose, three experimental series were carried out using the material of the tasks we developed: «Letter-digit correspondences», «Moving a chess piece», «Who is older? Who is younger?».
These tasks were offered to children studying in the first, second and third grades according to experimental and regular programs for elementary grades.
The results obtained showed that teaching first, second and third grade schoolchildren according to experimental programs, as opposed to teaching according to regular programs, creates significantly more favorable opportunities for children to master theoretical-type thinking.
The scientific meaning of the work carried out is that its results contribute to the expansion and specification of the provisions of psychological science that characterize the peculiarities of mastering theoretical-type thinking by children aged 6-10 years when studying according to different programs.
The practical meaning of the work carried out is to test the methods “Letter-digital correspondences”, “Moving a chess piece”, «Who is older? Who is younger?», which can be used in diagnosing theoretical thinking in children aged 6–10 years, in particular to establish the formation of educational results of a meta-subject nature [4].
References
1. Davydov V.V.Theory of developmental learning. Moscow:Intor,1996.544 p.2. Zak. A.Z. Diagnostics of differences in the thinking of younger students: Assessment of readiness for primary and secondary school: Development control in the period 6-10 years. Moscow: Genesis, 2007. 159 p.
3. Rubinstein S.L. Fundamentals of General Psychology. St. Petersburg: Piter, 2019. 720 p.
4. Federal state educational standard of basic general education. FSES. Moscow: Prosveshchenie, 2019. 61 p.
