1. Introduction

Developed in the 21st century, Federal State Educational Standard of Basic General Education [6] contains important provisions that prescribe the need to achieve cognitive meta-subject educational results in secondary school, which are formed as children master a number of cognitive competencies. The main competencies are those associated, firstly, with the ability to develop effective ways to solve educational and cognitive tasks, as well as problems of a search nature, secondly, with the ability to plan ways to achieve goals, and thirdly, with the ability to carry out cognitive reflection when solving various problems.

When developing the characteristics of the noted cognitive competencies, we were based on the provisions on the types of cognitive activity developed in dialectical logic [4] and implemented in the works of V.V. Davydov [1] and his followers [2], [3], [5].

Based on these provisions, it can be argued that human cognitive activity has two forms. In one case, the activity of the subject of cognition is aimed at reflecting the internal relations of phenomena, understanding the causes of their changes and is characterized as meaningful, reasonable cognition. In another case, this activity is associated with the description of the perceived features of cognizable phenomena.

1.1. Types of problem solving method

The noted characteristics of the types of cognitive activity suggest that in one case, the development of a method for solving problems is associated with significant relationships of data contained in the conditions of the problems. In the first case, on the basis of identifying essential relations, conditions are created for developing a general method for solving all problems of a certain class, and in the second case, there are no such conditions and it is possible to develop only a particular method for solving one or more problems of this class [1].

It should be noted that the development of a method for solving a problem is based on an analysis of its conditions, which (depending on which method is being developed) can be meaningful or formal. In the first case, the analysis of the problem is associated with the disclosure of the essential relationships of the data presented in its condition. This allows us to successfully solve all the problems of the proposed class. In the second case, essential relations are not singled out during the analysis of the problem. Therefore, all problems of the proposed class cannot be solved successfully — this is possible only with respect to individual problems.

The noted characteristics of different types of analysis underlie the development of research and diagnostic experimental situations. So, to determine the type of analysis of the conditions of the proposed problems and, accordingly, the nature of the method used in solving them, it is necessary that a child or an adult solve several problems of the same class (i.e., problems built on the basis of a single principle). In this case, the observed features of the conditions of these problems should be different.

1.2. Types of reflection in solving problems

Based on the noted provisions of dialectical logic, it was assumed that cognitive reflection in solving problems can be associated, in one case, with the child’s appeal only to the external features of the methods of action, in the other case, with an appeal to the foundations of his own methods of action, with finding out why you have to do it this way and not the other way. In the first case, it is believed that cognitive reflection is carried out as a formal action that does not reveal the reasons for choosing the implemented method of action, in the second case, as a meaningful action.

To establish what type of reflection is formed in a student, it is first necessary to offer him to solve several tasks, selected so that some of the tasks belong to one class, and the other part of the tasks to another. Then, after successfully solving all the proposed tasks, they need to be grouped. According to the grouping performed by the student, it was possible to judge what kind of cognitive reflection was carried out when solving problems.

If the tasks were combined on the basis of the commonality of the principles of their construction (that is, by belonging to the same class), then it could be assumed that meaningful cognitive reflection took place. If the tasks were combined on the basis of the external similarity of the observed features of their conditions, then it was assumed in this case that in solving the tasks the student carried out formal cognitive reflection. If the student did not solve all the problems correctly (despite the fact that he combined them either on internal grounds or on external characteristics), then this indicated the absence of any kind of reflection in solving problems.

1.3. Types of planning for solving problems

Like the cognitive competencies discussed above, two types are also distinguished in planning. In one case, the search for a solution to the problem is associated with the development of a program for the implementation of all necessary actions to achieve the goal, in full. In another case, the program is developed in parts, with each part being implemented separately, and the next part of the program is scheduled only after the implementation of the previous part. In the first case, planning is characterized by completeness and integrity, in the second case, by fragmentation and partiality.

The type of planning was determined in two stages. At the first stage, the student was asked to learn how to perform a simple action. At the second stage, he needed to cope with several tasks (four, six or eight tasks) so that when solving them, he had to perform sequences of such actions. At the same time, such tasks were selected so that the number of actions mastered at the first stage gradually (from task to task) increased, so that there were at least two tasks with the same number of required actions, and so that all the proposed tasks did not have a common solution method. The last requirement is due to the fact that the student, when solving each problem, could not use the method of solving the previous one, but had to draw up a new program of actions each time to solve the problem.

 If the student managed to solve all the proposed tasks, then in this case it was assumed that he carried out holistic planning, when the entire sequence of actions necessary to obtain the required result is outlined. If it could not cope with tasks where it is required to find a sequence composed of a relatively large number of actions, then in this case it was assumed that it carried out only partial planning, when each action is planned and performed separately.

To determine the features of the formation of cognitive meta-subject competencies in seventh graders related to the development of a method for solving problems, with planning and cognitive reflection, we used the “Repetition” technique developed by us earlier [3].

2. Materials and methods

A diagnostic lesson using this technique is carried out with a group of children. In particular, two groups of seventh-graders participated in our study — a total of 51 people. The diagnosis was carried out twice: at the beginning of the academic year (September) and at the end (May).

2.1.Features of conducting a diagnostic lesson

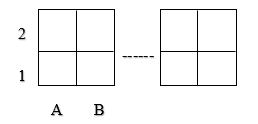
The diagnostic session is carried out as follows. In the first minutes of the lesson, students are given answer sheets so that they indicate their last name. After that, an image of the playing fields is placed on the blackboard (Fig. 1).

One playing field, on the left, is considered the initial one, since its cells contain letters that can be mentally interchanged, and the other playing field, on the right, is considered the final one, since its cells contain numbers that act as an example of the arrangement that must be obtained by swapping letters. Numbers are located to the left of the initial field, and letters are located below. Thanks to this notation, each cell of the playing field has its own name from a letter and a number, for example, B2 is in the upper right corner of the square, A1 is in the lower left corner, etc.

Fig. 1. Playing fields

The teacher (or educational psychologist) conducting the diagnostic lesson explains to the students the notation of the playing field: “Two squares are drawn on the board. Each square has four cells. Each cell has a name made up of a letter and a number. The two cells at the top of the square are called A2 and B2, and the two cells at the bottom are called A1 and B1”.

After that, two letters P are placed in the cells on the left in the initial playing field, and two letters M are placed in the cells on the right. In the final playing field, the numbers 8 are placed in the two upper cells, and the numbers 5 are placed in the two lower cells. Thus, in the initial playing field there are letters that can move, and in the final playing field there are numbers that do not move — their location acts as a model for the location of the letters after a certain number of their movements (Fig. 2).

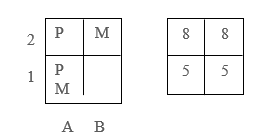
Figure 2. Conditions of a simple task

Further, the teacher notes: “The meaning of this task is to swap some two letters among themselves in such a way that the same letters would be in the same cells where the same numbers are located. Which letters do you think should be swapped?”

After discussing possible options for exchanging letters in places, the teacher demonstrates how to formulate a solution to the problem in one action: for this, to the right of the condition of the problem, he writes: 1) A1 — B2 or 1) A2 — B1 (Fig. 3).

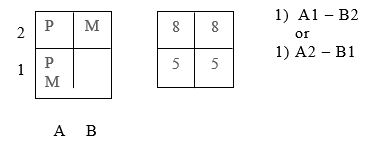
    Figure 3. Solving a simple problem

Having made the indicated record of the solution to this problem, the teacher reveals the meaning of the actions performed: “When we swap the letters from cells A1 and B2, then in this case the same letters will be in the same cells where the same numbers are located: two letters M will be in the same cells , where the numbers are 5, and two letters P will be where the two numbers are 8. This solution is written as follows: A1 — B2. If we act differently and swap the letters in cells A2 and B1, then in this case two letters P will be where the two numbers are 5, and two letters M will be where the numbers are 8. This solution is written differently than former: 1) A2 — B1.

After that, the children are offered the condition of another, more complex problem, where the solution consists of two actions of the simultaneous exchange of places of two letters (Fig. 4).

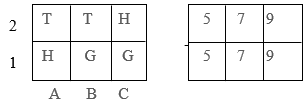
         Figure 4. Complex task conditions

Turning to schoolchildren, the teacher says: “In this task, it is required to find such two actions so that as a result the same letters end up in the same cells where the same numbers are located.”

Next, the teacher organizes a discussion of possible options for the first and second actions and then shows one of the correct solutions, in particular: 1) A2 — B2; 2) B2 — C1.

Then he reveals the meaning of this solution: “In this solution, the first action is that we swap the letters T and H in the upper cells of the rectangle, A2 and B2. As a result, two letters H will be in the same cells where there are two numbers 5.

The second action is that we swap the Letters T and G in cells C2 and B1. As a result, two letters T will be in the same cells where there are numbers 9, and two letters G will be where there are numbers 7. So, as a result of these two actions, the same letters are in the same cells where the same numbers are located. Of course, other solutions are also possible. When you solve such problems, remember that you need to write down only one solution.

After that, the students are given sheets with the conditions of 12 problems (Fig. 5).

       TASK 1

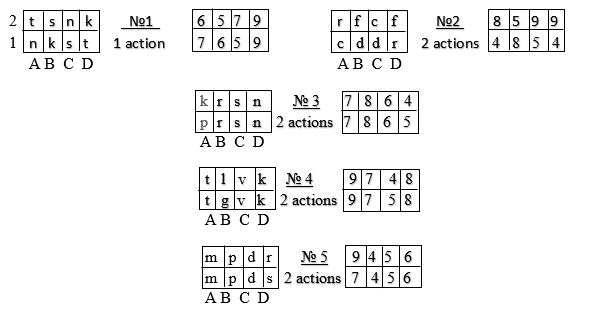
Problems opinions

Several grade 4 students solved these problems and exchanged opinions.

Tanya said: «Problems 3, 4 and 5 are similar.»

Kolya disagreed: «Problems 3, 4 and 5 are different.»

Vika: “I think that tasks 3 and 4 are similar, but task 5 is different from them.”

Katya: “I think that tasks 3 and 5 are similar, but task 4 is different from them.”

Nina: “I’m sure that tasks 4 and 5 are similar, but task 3 is different from them.”

Which student is right?

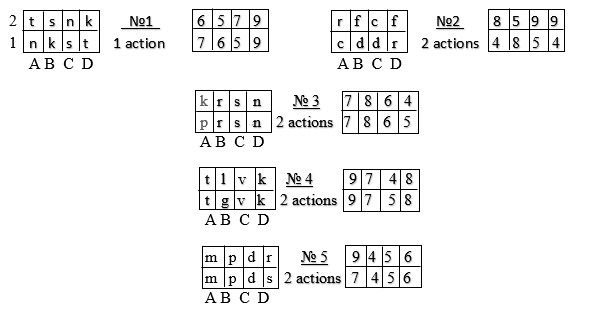
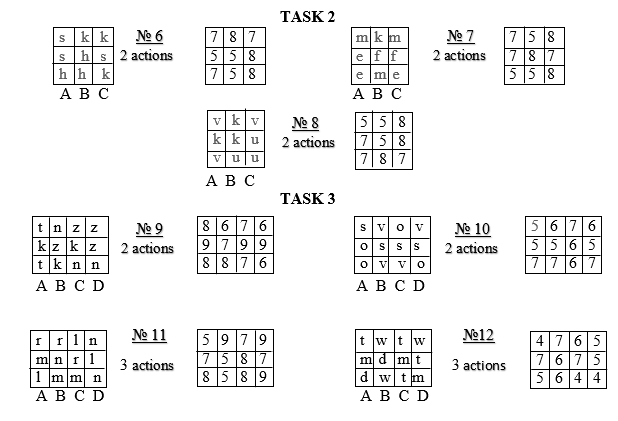
Figure 5. Task conditions for tasks 1, 2 and 3

Next, the teacher explains the location of the tasks on the sheet: “Look at the sheet with the tasks. In the first task, you first need to solve problems No. 1 and 2, and then problems No. 3, 4 and 5. After that, you need to read the students’ opinions about these three tasks and on the answer sheet select and mark the name of the student whose opinion is the most correct for you . In the second task, you need to solve three problems in two steps. In the third task, you need to solve 4 tasks: two tasks in two actions and two — in three actions”.

At the end of the instruction, the children are told:

“Solve problems in a row, starting with the first:

— do not copy the conditions of the tasks;

— look for and write down only one solution;

— you can not make any notes on the sheet with the conditions of the tasks, as well as on the table and any pieces of paper.

Solve problems only mentally, in the mind, as examples for addition in mental counting. Act carefully and independently”.

2.2. Evaluation of the results of solving problems

When processing the results of solving problems, one should be based on the following provisions.

The meaning of task 1 is to determine the type of cognitive reflection in solving problems. For this, schoolchildren need to solve tasks 3, 4 and 5 (two tasks, — 3 and 5, are built according to one principle, one — task 4 — according to another) and choose one opinion about them from five proposed ones (tasks 1 and 2 act as practice).

If, having correctly solved these three tasks, the child chooses the 1st, 2nd, 3rd or 5th opinion, then in this case it was believed that formal cognitive reflection took place during the solution. If the fourth opinion was chosen, then this testified to the implementation of meaningful cognitive reflection.

When one or two of these three tasks, or even all three, were incorrectly solved, this indicated the absence of any kind of reflection in solving these problems.

The meaning of task 2 is to determine which method of solution — general or particular — was used in solving problems 6, 7 and 8, which are built according to a single principle. If the student coped with all three tasks, then this indicated that significant relationships were distinguished in their solution and, therefore, the general method was used. If the student did not cope with all three tasks, but solved two or one task correctly, then in this case it was considered that a particular method was used. In the case of an unsuccessful solution of all three tasks, it was assumed that there was no development of the method at all, the student acted at random.

The meaning of task 3 is to determine the type of planning when solving problems 9, 10, 11 and 12. These four problems differ from the previous ones in that when solving them, one should mentally operate with a larger number of elements (letters and numbers) than before. If the student could not solve all four problems correctly, then this indicated the absence of a program of action for solving these problems.

If the student coped with one, two or three of these four tasks, then this indicated that partial planning was used in solving them, when it was not possible to immediately construct the entire sequence of necessary actions. If the student coped successfully with all four tasks, then this testified to that. that when solving them, holistic planning was used, when the entire sequence of required actions is outlined before the first action is performed.

3. Results.

As noted, 51 seventh grade students participated in the study. The results of solving the problems of the «Repetition» methodology at the beginning and end of the academic year are presented in the table.

Table

The results of solving the problems of the «Repetition» technique by seventh grade students at the beginning (September) and end (May) of the school year

Note: *p<0.05.

Based on the data presented in the table, the following can be noted. Firstly, in September, the fewest students demonstrated the implementation of cognitive meaningful reflection when solving the proposed tasks of task 1 — 27.45%; most of all — solving problems in a general way, included in task 2 — 70.59%.

It is important to note that in September the total number of students who demonstrated tasks 1 and 3 when solving tasks — 58.82%, was less than the number of students who solved tasks in a general way — 70.59%.

Secondly, in May, as well as in September, the fewest students demonstrated the implementation of cognitive meaningful reflection when solving the proposed tasks of task 1 — 39.22%; most of all — solving the tasks included in task 2 in a general way — 78.83%.

However, in contrast to the results obtained in September, the total number of students who demonstrated when solving problems of tasks 1 and 3 — 88.24% became more than the number of students who solved the tasks of tasks 2 in a general way — 78, 83%.

Thirdly, comparing the results of solving tasks of tasks 1, 2 and 3 in September and May, it should be noted that the least increase was in the number of students who, when completing task 2, demonstrated the solution of problems in a general way — 70.59% and 78.83%; most of all, the number of students who demonstrated problem solving with the help of a holistic planning of their actions increased the most — 31.37% and 49.02% — here it is important to note that the difference between the last indicated indicators is statistically significant (at p < 0.05).

The noted results indicate that seventh grade education contributes more to the formation of a holistic planning among schoolchildren, and to a lesser extent to the formation of a common way of solving problems.

4. Discussion.

This study was devoted to the study of the fundamental problem of developmental and educational psychology: learning and development.

In particular, it was necessary to find out how, in the course of studying in the seventh grade of secondary school, adolescents form important cognitive competencies related, firstly, to the ability to develop effective ways to solve educational and cognitive tasks, as well as search problems, and secondly, with the ability to plan ways to achieve goals, thirdly, with the ability to carry out cognitive reflection in solving various problems.

When conducting group experiments, we used the technique » Repetition » developed by us. The technique included spatial-combinatorial tasks, in the solution of which it was necessary to bring the initial state and the required state of objects into conformity — the arrangement of letters had to be brought into line with the arrangement of numbers.

To determine the features of the formation of the three cognitive competencies in schoolchildren in the course of studying in the seventh grade, three tasks of the “Repetition” methodology were used. The first task was intended to determine the nature of the formation of the ability to solve problems using cognitive meaningful reflection — the task included 5 tasks. The second task was intended to determine the nature of the formation of the ability to solve problems in a general way — the task included 3 tasks. The third task was intended to determine the nature of the formation of the ability to apply holistic planning in solving problems solving problems — the task included 4 tasks.

1.Limitations of the study

The results obtained in the study have limitations, in nature, since the sample of seventh graders was relatively small — only 51 people. Also, certain limitations for the interpretation of the data obtained are associated with the use of a specific methodology, in which children are offered three tasks, including a total of 12 spatial-combinatorial tasks that are solved in a visual-figurative form.

It can be assumed that if schoolchildren were offered to solve the same problems, but in a subject-effective form (for example, on cards with letters and numbers) under the conditions of an individual experiment, then the results of solving problems would differ from those obtained in this study.

The results would be different even if schoolchildren were asked to solve plot-logical problems in a verbal-sign form.

2.Directions for future research

It is planned to conduct a study on the material of the «Repetition» methodology with younger children — with students in grades 5 and 6 and with older children — with students in grades 8 and 9.

It is supposed to carry out the research again with a sample of seventh-graders, but at the same time, the children will be offered the spatial-combinatorial tasks of the «Repetition” technique, solved in a subject-effective form under the conditions of an individual experiment.

It is of serious research interest to conduct a study in which seventh-graders will solve other types of problems, in particular, plot-logical ones.

5.Conclusion.

So, in the study, which is related to the determination of the formation of cognitive competencies in seventh graders, it was shown for the first time that the most intensively formed at this age cognitive competence, reflecting the features of problem solving planning.