1.Introduction.

When studying the thinking of younger schoolchildren (see, for example, A. Z. Zak [3 ]), we proceeded from the fact that theoretical thinking (as aimed at reflecting essential relations in the tasks being solved) is carried out in different ways depending on the content of these relations: the general principle of solving problems of a certain class (universal), the specific principles for solving subclasses of problems of this class (special) or the unity of the general and specific principles (the unity of the universal and the special, the whole).

In this case, it was supposed, in particular. that the development of theoretical thinking at primary school age consists in the assimilation of its initial forms by children, i.e. in the formation of schoolchildren’s opportunities for solving problems in analytical and reflexive ways in a subject-effective plan.

This study is based on the assumption that the development of theoretical thinking in middle and high school consists in the development of its developed forms by students, thanks to which they have the opportunity to solve problems in analytical and reflexive ways in visual-figurative and verbal-sign terms.

In our studies (see, for example, [4 ]), it was shown that when teaching in elementary school, favorable opportunities are created for children to master generalized methods of action that involve distinguishing between essential and non-essential data in the tasks being solved, i.e. e. to form in children the initial forms of a meaningful, theoretical approach to solving problems.

Based on the characteristics of the content of education in the middle and high school, it can be assumed that the age period of 10-17 years is a natural stage in the ontogenetic development of thinking, the content of which is the formation of developed structures of comprehending, theoretical thinking.

It should be noted that, according to the provisions of dialectical logic [ 1], theoretical thinking, considered as an action to form the concept of cognizable objects, should (include the consistent solution of such problems as highlighting in cognizable objects, first certainty, denoted by the category of the universal, then — certainty , denoted by the category of the special, and, in conclusion, the allocation of certainty, denoted by the category of the individual, the whole as a unity of the universal and the special.

It can be said, therefore, that the isolation of a general relation is a necessary condition for the selection of special forms of a general relation. In turn, the solution of this problem is a necessary condition for highlighting the unity of the universal relation and its special forms and, thereby, achieving the ultimate goal of theoretical thinking — the formation of the concept as the unity of the universal, particular and singular.

 The noted characteristic of the certainties that a person distinguishes in cognizable objects at three stages of concept formation allows concretizing the content of his thinking in the following way.

At the first stage, the study of cognizable objects is associated with the allocation of a relationship that is universal for their existence, and the consideration of the characteristic features of this allocation is associated with an assessment of how essential and universal this relationship is.

At the second stage, the study of objects is associated with the identification of special forms of the previously discovered universal relationship, and the consideration of the features of this separation is associated with an assessment of how specific and isolated these special forms are.

At the third stage, the study of objects is connected with the identification of the unity of the universal relation and its special forms, and the consideration of the features of this separation is with an assessment of how real this unity is, to what extent the totality of special forms exhausts the general relation.

From a psychological point of view, in particular, within the framework of the theory of activity of A.N. Leontiev [2 ], theoretical thinking is a complex cognitive action. In the course of its implementation, a person successively, with the help of appropriate methods, first singles out in cognizable objects a relationship that is universal for their existence, then special forms of this relationship and, further, singles out the unity of the universal relationship and its special forms, i.e. singular, whole.

Methods of theoretical thinking are carried out with the help of the study of cognizable objects and consideration of the features of this study, in particular in relation to the content of the problem being solved.

So, in the original method, analysis is the leading one, since its result directly coincides with the result of the whole action. Reflection plays a supporting role here.

Such an interaction of these acts is characteristic of a person’s transition from reflecting a phenomenon to reflecting an essence: “The lack of reflection is characteristic of the analytical stage of cognition, when separate abstractions are singled out from the whole” [1, p.116]. This method is characterized as analytical.

In the next method, the situation is different: reflection is the leading one, since without reflecting the differences in the analysis of the various components of the content of tasks, the result of this action cannot be obtained. This way of theoretical thinking is characterized as reflexive.

When highlighting the unity of the universal and the particular, analysis and reflection equally ensure the successful implementation of this method. This method is characterized as synthesizing.

Considering the development of these methods as stages in the development of theoretical thinking, it is advisable to refer to the provisions of the theory of A. N. Leontiev [2 ] about the transformations of the components of objective activity.

At the same time, while developing the general scheme of the experimental situation, which could be embodied in various concrete materials, we also relied on the logical characteristics of theoretical thinking.

Firstly, the subject must be offered to solve not one, but several tasks objectively of the same class. At the same time, the observed features of the conditions of the proposed problems should differ quite clearly. Compliance with this requirement when constructing a specific technique will allow, with the successful solution of such problems, to observe the fact of a theoretical approach to their solution, which is implemented, in particular, by implementing the analytical method of theoretical thinking.

Secondly, the proposed tasks should objectively relate to different subclasses of this class. This will make it possible, if all problems are successfully solved, to observe a meaningful grouping of problems, the basis of which is taken to be their objective belonging to different subclasses of the same class. This fact, according to our ideas, should testify to the implementation of the reflexive method of theoretical thinking.

Thirdly, it is expedient to select such a class of problems, in relation to which it was possible to develop problems not of two, but of several subclasses. In this case, opportunities are created for the successful solution of the proposed tasks and the allocation of tasks of different subclasses to observe the production of a new subclass of tasks of this class by a person. In the presence of such a fact, it can be assumed that, solving the proposed problems, he fulfilled not only the analytical and reflexive methods of theoretical thinking, but also the synthesizing one.

Thus, the general research strategy of our experiments in the study of theoretical thinking was to describe the typical procedural characteristics of mental activity, corresponding to corresponding to one result or another. In other words, the research task was to highlight the characteristics of the analytical, reflexive and synthesizing modes of theoretical thinking.

2.Materials and methods.

The experiments of this study were aimed at clarifying how, when solving problems in a verbal-sign form, there is a transition from orientation in their conditions using the analytical method of theoretical thinking to orientation using its reflexive method and, most importantly, to orientation using its synthesizing method in schoolchildren of 5-11 grades.

The “Difference-Coincidence” method was used, which is a variant of the “Different-Same” method, which was used earlier [  5  ] when studying the transition of middle and high school students from orientation in task conditions using the empirical method to orientation using analytical method of theoretical thinking in solving plot-logical problems.

The “Difference-Coincidence” methodology is constructed in such a way that these two subclasses of problems (two problems in one subclass and one in another) do not exhaust all subclasses of problems of the proposed class. The subject has the opportunity, having successfully solved all the problems and having singled out both subclasses among them, to offer at least one more subclass of problems, i.e., to single out one more special form of the existence of a general relation. This will testify to the fact that when solving problems, a synthesizing method of theoretical thinking was used, characterized by the allocation in the content of problems of the unity of the general relation and its special forms.

Thus, this technique makes it possible to distinguish by what method of theoretical thinking the problems were solved — analytical, reflexive or synthesizing. 30 students of the fifth, 29 of the sixth, 28 of the seventh, 29 of the eighth, 30 of the ninth, 31 of the tenth, 32 of the eleventh grade participated in solving the main problems in individual experiments.

The experiment with each student included four stages and lasted, on average, 30-40 minutes. At the first stage, three training tasks were solved, at the second, three main tasks were solved, at the third, a task was performed related to the formulation and substantiation of judgments about successfully solved main tasks, at the fourth, a task was performed, consisting in self-compilation of tasks.

2.1. The first stage of the experiment

The student was given a form with the conditions of three training problems — A, B and C. On this form it was necessary to write the answer to each problem. In addition, it was allowed to make various kinds of notes directly in the text of the problem conditions. Along with the form, a blank sheet of paper was given on which the student could make some notes in the course of solving these problems.

Training problems

Problem A: “Vanya, Petya and Seryozha play musical instruments. Some of them play the trumpet, some play the flute, some play the trumpet. Petya and Vanya play different instruments, Vanya and Seryozha play different instruments. Who plays the flute?” (Answer: Vanya).

Problem B: “Ira, Masha, Marina and Katya knitted things from wool. One of them knitted a hat, another knitted a hat, one knitted a scarf and one knitted a hat. Masha and Katya knitted different things, Masha and Marina also knitted different things. Which girl knitted a scarf?” (Answer: Masha).

Problem C: “Misha, Vitya, Vasya and Kolya were picking mushrooms. One of them collected mushrooms, one — russula, one — mushrooms, one — boletus. Vitya and Kolya were picking different mushrooms, Misha was picking aspen mushrooms, Vitya and Vasya were picking different mushrooms. Who collected russula?» (Answer: Vitya).

The marked training tasks were chosen based on the following considerations. The solution of problem A was necessary in order for the student to be able to operate with the original for the entire class of problems (presented in the “Different — the same” and “Difference — coincidence” methods), the ratio of the number of these objects to the number of their proposed properties: if out of three objects, — A, B, C, — two have the property «X», and one has the property «Y», and if objects A and B, B and C have a different property, then, therefore, objects A and C have the property «X», and object B — property «Y».

The solution of problem B allowed the student to apply the specified initial relation in a situation with redundant information. The solution of problem C was necessary so that the doctrine could try to operate with the initial relation in a situation where these objects have three properties, and not two, as in problems A and B.

In the course of solving training problems, the student read the problem himself (silently or aloud). The experimenter helped with difficulties, both at the stage of understanding the text of the conditions of the problems (recommending to schematically depict the relationship between the characters of the problem and their properties), and at the stage of their solution. In the latter case, he offered questions that help the student understand the following actions: how to start solving the problem, as reported in the first part of the problem, what follows from the judgments presented in the second part, what you need to know in order to answer the question of the problem.

2.2. The second stage of the experiment

After the student solved (on his own or with the help) the training tasks, he was asked to solve the main tasks 1, 2 and 3.

Main problems

1. Petya, Vova, Misha, Igor and Oleg wrote an algebra test. One of them got a five, one got a three, one got a four, one got a two, one got a five. Vova and Misha got a different mark, Petya — a three, Igor and Vova — a different mark, Oleg — a two. What grade did Vova get? (Answer: Vova got a four).
2. Katya, Sveta, Lisa, Rita and Natasha lived far from the school. One of them was on a bus, one on a tram, one on a bus, one on a tram, one on a bus. Sveta and Rita rode different modes of transport, Katya rode a bus, Natasha and Rita rode different modes of transport, Liza rode a tram. What was Rita driving? (Answer: Rita rode the tram).
3. Fedya, Masha, Kolya, Larisa and Zhenya are preschoolers. Some of them were in the middle group, some were in the junior group, some were in the preparatory group, some were in the middle group, and some were in the senior group. Kolya and Larisa were in different groups, Zhenya was in the younger one, Masha and Kolya were in different ones, Fedya was in the preparatory one. Where was Kolya? (Answer: Kolya was in the senior group).

The solution of the main tasks was organized in the same way as the solution of the training ones. The student was given a form with the main tasks (where it was required to write answers and allowed to make notes) and a blank sheet of paper for various kinds of notes.

2.3. The third stage of the experiment

After successfully completing the three main tasks, the student had to choose one of the five opinions about these tasks and then justify his choice.

Opinions

1. All main tasks are similar.
2. All the main tasks are different.
3. The first and 2nd main tasks are similar, but the 3rd one differs from them.
4. The first and 3rd main tasks are similar, but the 2nd one differs from them.
5. The second and 3rd main tasks are similar, but the 1st one differs from them.

                                                *   *   *

According to the results of the grouping of successfully solved main tasks, the subjects were divided into four groups — A, B, C and D.

2.3.1. Characteristics of the actions of students of the first group

The first group (out of those named) included students who characterized problems on the basis of the external features of their conditions, i.e., those who acted empirically in solving them.

Part of the subjects of group A (subgroup A1) chose the first opinion, justifying this by the fact that «… in all tasks there are 5 people …» or «… in each task it is said about those who have different …». The other part of the subjects of group A (subgroup A2) chose the second opinion, based on the fact that «… in all tasks they talk about different things — school, buses, pens …» or «… in each task there are different children — in the first, boys, in the second, girls , in the third preschoolers … «. It should be noted that in all classes from 5 to 11 the number of marked subgroups is approximately the same.

Observations of the actions of the subjects of group A (especially during the solution of the first main task) made it possible to note a number of characteristic features that were reproduced to the same or less degree in the solution of subsequent tasks.

So, some students (subgroup A1) tried immediately, after the first reading, to give an answer to the question of the problem, saying that «… Vova received three …». At the same time, as it turned out, they were based on the coincidence of the order of the characters (in the first sentence of the problem) and their assessments (in the second sentence). After receiving an indication that the answer was wrong, they proceeded to repeatedly read the problem, trying to understand its meaning. It should be noted that such students met only in the fifth grade and constituted an insignificant part of group A.

Other students (they were in all classes and made up the majority in this group — subgroup A2) first read the problem many times, trying to learn its condition. One part of the students of subgroup A2 after that offered a solution based on their impression of the given data (and not on the basis of reasoning), believing that Vova got five because “… Petya had a three, Oleg had a two and there are still two fives left … «. Such students were a minority of subgroup A2 and were only in the fifth and sixth grades.

The second part of the students of subgroup A2, in the course of repeated reading, singled out (circled with a pen) those characters whose assessment was known (“Petya — three”, “Oleg — two”). After that, they tried to understand what the remaining judgments meant (“Vova and Misha received a different assessment” and “Igor and Vova — a different assessment”), and could not independently compare and draw a conclusion. Such students made up the majority of the A2 subgroup in the fifth through sixth grades, half in the seventh grade, a minority in the eighth grade, and were absent in the upper grades.

The third part of the students of subgroup A2, after repeatedly reading the problem and separating known data from unknown ones, did not try to derive an answer, but tried to pick it up, comparing the remaining two judgments. Some students said, for example, like this: “… If Vova got five, then Misha got four. …This is not at odds with the conditions. So, Vova — five … «. When the experimenter reported that this was not true, the students easily agreed with this and said «… then Vova — four …». Other students of this subgroup spoke differently: “… If Vova got four, then Petya got five. So, Vova — four … «.

Thus, for the third part of the students of subgroup A2, as can be seen, it was typical to consider only one of the two judgments. Some even considered the second judgment (“Igor and Vova received different marks”) as superfluous, sometimes saying “… why is this, if it is already clear that Vova received four …”.

The students of the fourth part of the A2 subgroup, after repeatedly reading the problem and separating the known from the unknown, did not try (unlike the students of the third part of the A2 subgroup) to operate with only one of the judgments characterizing the difference in the properties of the proposed pairs, but compared both of these judgments and, as a rule, did not quickly, but still correctly, they made, for example, the following conclusion: “… if Vova and Misha have different grades, and Vova and Igor have different grades…, and only two fives and one four remain…, then Misha and Igor have the same grades, fives , and Vova has a four … «.

In conclusion, it should be noted that students who used the selection of an answer (the third part of subgroup A2) and reasoning by comparing both judgments (the fourth part of subgroup A2) in solving problems were in all classes. However, their numbers in this subgroup steadily increased and in the upper grades they made up a significant majority of the A2 subgroup (and, consequently, of the entire A group, since the students who made up the A1 subgroup were only in the fifth grade).

In addition, it should be pointed out that the students of the named parts of subgroup A2 retained the noted methods of mental activity in solving both subsequent tasks. At the same time, their preliminary orientation in the conditions of the problems was reduced slightly, since they also read the conditions of the problems many times and circled the known data with a line.

2.3.2. Characteristics of the actions of students of the second group

The second group (group B) included subjects who chose the first opinion, since “… in each task there are three people, where one differs from the other two …” or “… everywhere it is said first that two children have something different, then two more and it is clear that one is different from the two … «.

This testified to the fact that when solving problems they acted in an analytical way of theoretical thinking, since they characterized problems on the basis of a single meaningful approach. Thus, they pointed to the significant generality of the solution of problems of the proposed class, since its construction is really based on the ratio of the number of these objects and the number of their proposed properties — in each task, the conclusion is made on the basis of a comparison of pairs of characters with different properties: in the first task — this is Vova with Misha and Igor with Vova, in the second problem — Sveta with Rita and Natasha with Rita, in the third problem — Kolya with Larisa and Masha with Kolya.

 Observations of the actions of the subjects of group B made it possible to note the following. Firstly, these students (unlike a number of subjects of the A2 subgroup) did not read the conditions of the tasks many times, but usually limited themselves to two or three readings (and in the senior classes, mostly two) and did not trace with a pen what was known (“Estimates of Petya and Oleg”), but simply said: “… it means that the three and two are already taken …”.

Secondly, they never used the selection of answers based on consideration of only one judgment about the nature of endowing a pair of characters with properties (“Vova and Misha received a different assessment”), but always compared both such judgments and made a consistent conclusion that Vova received a B .

They acted in the same way in solving the remaining two main problems, directing their attention, as one could see, to the selection of the conditions for the formulation of two judgments from the text, often noting that the rest was not important.

2.3.3. Characteristics of the actions of students of the third group

The third group (group B) included subjects who acted in a reflexive way of theoretical thinking, because, justifying the fourth judgment they chose, they managed to reveal a significant difference in the implementation of the general method for constructing and solving all these problems, to highlight the typical features of the method that provides with the need to successfully solve problems of different subclasses.

At the same time, one part of the students (subgroup B1) expressed a judgment about the commonality of tasks 1 and 3 in a more specific form, for example: “… in the first task there are four types of assessments and in the third four types of groups in kindergarten, and in the second there are only two types of transport, bus and tram…», and the other part of the students (subgroup B2) in a less specific form, for example: «… in the first and third tasks there are many different ones, and in the second — few…».

Thus, the subjects of group B identified two subclasses among the tasks of the proposed class: the first and third tasks were built on the basis of one type of initial relation (i.e., the ratio of the number of given objects to the number of proposed properties), which manifests itself in the fact that five objects are endowed with four properties, and the second task — based on a different kind of initial relationship — in this case, five objects are endowed with two properties.

Thus, the students of this group managed to reveal a significant difference in the implementation of the general method for constructing and solving all these problems, to highlight the typical features of the method that, with the need, ensure the successful solution of problems of different subclasses.

It is important to note that in the fifth, sixth, seventh and eighth grades, among the subjects of the group under discussion, students from the B1 subgroup prevailed, in the ninth grade the number of subgroups B1 and B2 was almost the same, and in the tenth — eleventh grades the students of the B2 subgroup prevailed.

Observations of the actions of the subjects of group C made it possible to note that, along with the actions characteristic of the subjects of group B (identifying two judgments in the text of tasks and operating with them in the course of reasoning), when faced with the third task, they quickly discovered its relationship with the first, noting those points that they then expressed as justification for their choice of the fourth opinion, pointing out, in particular, four types of preschool groups in the third task and four types of assessments in the first task.

2.3.4. Characteristics of the actions of students of the first group

The fourth group (Group G) included those subjects who were able not only to identify tasks of different subclasses, but also to compose new tasks. The experimenter suggested to them: “What task can you come up with so that five people do something, for example, catch different fish, or read different books, or take different exams, and so that the new task is not composed in the same way as the first with the third and not in the same way as how is the second one?”

The subjects of this group were able to propose tasks of another subclass, where a new kind of initial ratio of tasks of the proposed class was realized (i.e., the ratio of the number of given objects to the number of proposed properties), when five objects are endowed with three properties. It is interesting to note that, regardless of age, most often the students chose the plot with catching fish, using the number of fish caught as a comparable property in some cases, and the type of fish in others.

It should be noted that some of the subjects of this group (subgroup D1) offered tasks where five objects (for example, A, B, C, D, E) are endowed with three properties (for example, x, y, z) in such a way that three objects ( for example, A, B, C) have one property (for example, «x»), and the other two have others, for example: D belongs to the property «y», D — the property «z».

In particular, there was such a task: “Grisha, Vova, Misha, Seryozha and Zhenya were fishing. Three caught one fish each, one caught two fish and one caught three. Grisha and Vova caught a different number of fish, Vova and Misha — also a different number, Seryozha — one fish, Zhenya — three fish. How many fish did Vova catch?”

Another part of the subjects of this group (subgroup D2) offered tasks where five objects are also endowed with three properties, but these properties are distributed differently: two objects (for example, A and B) have one property (for example, the property «x»), two objects ( for example, C and D) are endowed with another property (for example, the property «y») and one object (for example, E) — with a third property (for example, the property «z»).

In particular, there was such a task: “Kolya, Vanya, Igor, Maxim and Alyosha were fishing. Two caught pike, two — ruff and one walleye. Kolya and Vanya caught different fish, Vanya and Igor — also different ones, Maxim — ruff, Alyosha — zander. Who did Vanya catch?” It is interesting to note that, regardless of age, students of the D1 subgroup prevailed in the D group.

Observations of problem solving by the subjects of group D (“synthesizing”) showed that their actions are characterized by the same features as the actions of the subjects of groups B and C (i.e., “analysts” and “reflexives”). At the same time, however, in contrast to the “reflexive” ones, the “synthesizers” actively reacted to the substantive difference between the second task and the first one, saying, as a rule, that “… it’s different here, there are only two types…” or “… this task is easier, only bus and tram… And when solving the third problem, they usually noted (after the first reading) that «… here again there are four types, … as in the first one …» or «… in this problem again there are more different things, as in the first one …».

3. Results.

The results of solving problems by schoolchildren in grades 5-11 are presented in the table.

Table.

Distribution of subjects with empirical (A), analytical (B), reflexive (C) and synthesizing (D) methods of solving plot-logical tasks in grades 5 – 11 (in%)

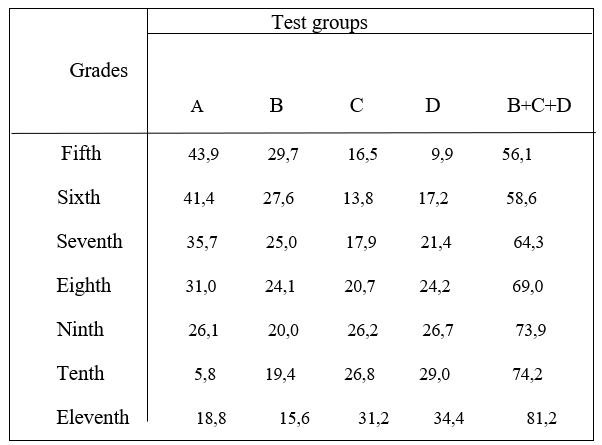
Analysis of the data presented in the table allows us to note the following. First, there is a relatively significant (by 7.3%) change, from grade 5 to grade 6, in the size of group D (ie, schoolchildren who acted in a synthesizing way). This happens, as can be seen from the table, due to a slight decrease in the number of group A («empiricists») — by 2.5%, group B («analysts») — by 2.1% and simultaneously with a very slight increase in the number of group B (“reflexive”) – by 2.7%.

Secondly, in grades 5–8 there are fewer “reflexives”, and in grades 9–11 there are more than “analysts”, and there are more “synthesizing” in all grades (except the fifth) than “reflexive”. At the same time, from grade 5 to grade 11, the number of “analysts” decreases, and the number of “reflexive” ones increases.

Thirdly, the proportion of “synthesizers” (Group D) among “theoreticians” (Group B + C + D) is increasing: in grade 5, the ratio of marked groups is 9.9% and 56.1% (i.e., the share of “synthesizing ” among the “theorists” is 18.8%), and in the 11th grade — 34.4% and 81.2% (i.e. the share of “synthesizers” among the “theorists” is already 42.4%).

4. Conclusion.

The study was aimed at studying changes in the nature of their orientation in schoolchildren from grades 5 to 11 in the conditions of solving plot-logical tasks in a verbal-sign form. In particular, of serious research interest was the question of when schoolchildren in grades 5-11 undergo a transition from orientation in the conditions of tasks using the analytical method of theoretical thinking to orientation using its reflexive method and, most importantly, to orientation using his synthesizing way.

A total of 209 schoolchildren enrolled in the fifth, sixth, seventh, eighth, ninth, tenth and eleventh grades participated in individual experiments.

The data obtained in the noted experiments and presented in the table indicate that during the period of study in grades 5-11, the theoretical method of solving plot-logical problems in its synthesizing form develops quite evenly. At the same time, it is important to note, as follows from the data presented in the table, that during the period of study in the middle and senior classes, the number of schoolchildren characterized by the implementation of the synthesizing method of theoretical thinking in solving problems is almost one third among graduates of a complete secondary school.

This gives reason to believe that the majority of peers will have the opportunity to solve plot-logical problems in a verbal-sign form in a synthesizing way of theoretical thinking only a few years after graduation.