1. Introduction.

In  modern economy are widely used various mathematical methods for solving practical problems, and theoretical modeling of socio -economic processes [1, 2]. Mathematical methods are an integral part of the methods of any section of economic science. The use of mathematical description of economic systems provides new opportunities for economic theory and practice development.

Information technology is a technological framework for the development of organizational and economic potential of rural areas [3-6]. It contains the following structural elements: mathematical modeling and forecasting of economic development, the means and methods of collecting, storing, processing and transmitting information to transactors of rural areas [7-13]. Information technologies, namely, mathematical models of production can evaluate its efficiency and minimize its costs. The most general answer to this question gives the law of diminishing returns, which is also called the «law of diminishing marginal product,» or «the law of changing proportions.» This law states that when a variable resource (e.g. labor) is successively accessed to a constant (fixed) resource of the firm (e.g., capital or land)  incremental or marginal product attributable to each additional unit of a variable source decreases from a certain point. If more workers are involved in the service of a fixed resource of production means, in the short run, the production volume growth will obviously be slower and slower with the increasing  number of the workers employed The law of diminishing returns also works in non-agricultural sectors. Imagine a small joiner’s workshop, making wooden frames. There is a certain amount of equipment such as lathe, planer and grinding machines, saws, etc. in the workshop If the firm hired only one or two workers, total output and the productivity level (output per worker) would be very low. These workers would have to perform many different operations. As a result the advantages of specialization would be lost. In addition, every time you moved the worker from one operation to another, you would loose working time, and the machines would mostly stand idle. In short, the workshop would work understaffed, and production would be inefficient because of the excess of capital compared with labor [14].

2. Materials and methods.

Based on the findings of economic theory, we see that the law of diminishing returns can be also applied within a short period of time. That is, if in the process of producing goods the units of a variable resource are added to fixed factors, from a certain point, each unit of a variable resource will add less value to the total product. In this regard, we distinguish four stages of the socio-economic system functioning within a short period of time..

The first and the second stages are associated with the increasing costs of variable resources and achievement of full employment of fixed resources

The third stage is intensive employment of fixed resources. The fourth stage is characterized by production efficiency decrease due to the use of excessive quantities of variable resources[15].

One should agree with the assertion that this law reflects the need to maintain the resource proportions. It is applicable to all manufacturing processes in socio-economic systems and all variable resources when at least one production resource is fixed. To understand the law and to follow it in conditions of limited resources means to contribute to the effectiveness of production, to achieve maximum output of goods at optimal distribution of factors between social and economic spheres.

Long-run period socio-economic system can change the volumes of all the resources used. Therefore, the function  of a long -run production is given in the form of isoquant (Fig. 1).

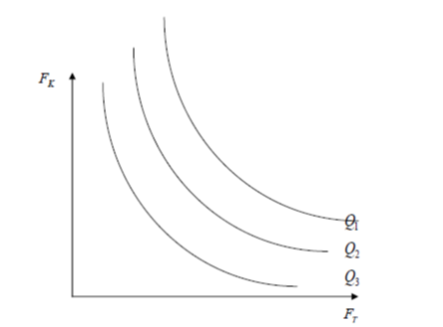
Figure 1. The oquants map of  socio-economic system

The graphs, showing  the isoquants of different volume of goods production are called isoquants map. At the same time:

Q₁, Q₂, Q₃ – isoquants of different output;

F_t – labor efforts;

F_k – capital employed.

Shown on the isoquant one and the same amount of goods with different combinations of production factors is achieved due to their interchangeability. When moving along the isoquant from top to bottom and from left to right simultaneously there is an increase of labor use (L), accompanied by a corresponding reduction of capital costs (K), i.e. the substitution of capital with labor. This substitution is characterized by the concept of «marginal rate of technological substitution of» labor’s capital:

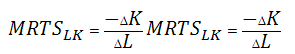  (1)

or

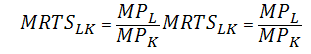(2)

Thus, interchangeability is a characteristic of production factors, which determines the possibilities of socio-economic system to choose the cheapest and the most available resource when creating social and economic benefits. These factors should be used to improve the functioning of the socio-economic system of rural areas.

Factors of production are not completely interchangeable, each factor performs its specific function, which another factor can perform worse or cannot perform .at all. .This implies another property of factors – complementarity. It means that the absence of one or more resources makes the process of goods production  impossible

To determine the equilibrium of production it is necessary to study the isocosts (Fig. 2).

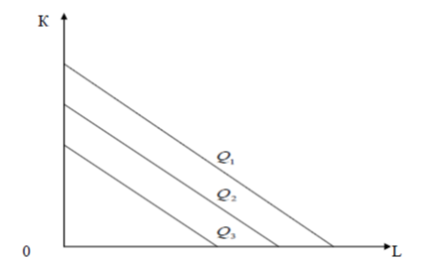
Figure 2. Socio-economic system isocosts

3. Results and discussion

Socio-economic system can spend a fixed amount of money on capital and labor employment because of the budget restraints. The budget system is represented with equation [2]:

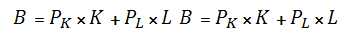(3)

where B is the budget system to purchase the factors;

P_k P_k   — price of  a capital unit

K —  amount of capital;

P_l P_l  —  price of a labor unit

L — amount of labor.

Thus, if you have a particular budget system you can theoretically use it to pay for labor services only or to purchase or to compensate capital value. Therefore, the relationship between production costs and the amount of labor and capital employed should be based on the equation of the line which provides the fact that any of these factors can be zero.

Isoquants and isocosts are combined with to determine the conditions of equilibrium. The point of their intersection is the optimal combination of resources [1, 2].

Taking into account that isoquant and isocost have the same slope at the point of intersection and  the isoquant slope is measured by the marginal rate of technological substitution and the slope of isocost is the ratio of resources prices, the equilibrium condition of the producer is written as follows:

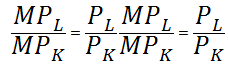(4)

Thus, the optimum combination of factors employed in benefits production process are achieved when the last ruble invested in the purchase of each factor yields the same gain in overall production of goods.

If the marginal product of one of the production factors  in monetary terms is bigger than the marginal product of other production factors , to minimize the costs of socio-economic system, it is advisable to reduce the quantity of the factor whose marginal product is smaller and to increase the quantity of the factor whose marginal product is bigger.

To calculate values you can use statistical methods, Lagrange multipliers method, and others.

It is advisable to optimize production factors for economic and social goods separately, as the volume of economic and social goods is stipulated not only due to the presence of  production factors  in rural areas, but also the method of their combination, which allows to describe these goods in two different functions.

It is clear that the status of territory resources depends on the state of  its fiscal position. Therefore, the activity of municipal and state authorities should be directed to creating the conditions providing increase of the resource potential, which means the growth of financial and tax potentials of the territory. These measures will contribute to the growth of the revenue base and budget revenues of rural areas [16].In such a situation managing position of the administration of the subject of the Russian Federation aimed at increasing areas activity for budget replenishment /17] is of great importance..

We use aggregate indices:

¾ — based on the fact that the increase in labor costs by1% will provide  ¾  increase of released goods;

¼ — based on the fact that the increase in capital inputs by 1% will provide ¼ increase of released goods.

Let economic benefits in the structure of expenditures be 10%, and social -15%. Accordingly, the total income is 100%. The share of economic goods in the overall structure is10 and social is 7 social.

Let    x1 – is   optimal amount of social goods;

x2 – is optimal amount of economic goods.

For the two goods a target consumption function is

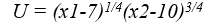
The price vector is P = (15; 10); net income is 100.

Marginal utilities — D = 100

Necessary optimum conditions give the following system of equations (λ is Lagrange multiplier):

((x2-10)3/4)/(4(x1-7)3/4) = 15λ

3/4((x1-7)1/4)/((x2-10)1/4) = 10λ

15×1 + 10×2 = 100

After substituting the first equation into the second we get:

3/4((x1-7)1/4)/((x2-10)1/4) = 10*(((x2-10)3/4)/(4(x1-7)3/4))/15

Expressed from the third equation, x1 and substituting in the last equality, we have:

3/4((-2/3×2-1/3)1/4)/((x2-10)1/4)-((x2-10)3/4)/(6(-2/3×2-1/3)3/4) = 0

Solving it relative to x2 will get: x₂ = ¹⁷/₈

When x₂ = ¹⁷/₈ or 2.125

x₁ = ²¹/₄ or 5.25

4. Conclusion

Thus, by setting the initial conditions of social and economic goods under the existing socio-economic system constraints, it is possible to determine their optimal ratio in the structure of consumption.