1. Introduction

Currently, more and more questions arise related to the distribution of many tasks to many resources (such as scheduling a task package for several processors or lecture schedules in classrooms). This is a common and important problem that can be formalized using a multi-agent approach.

Constraint processing can be seen as a broad and diverse field of research, combining methods and algorithms that span many different disciplines, including operations research, computer vision, artificial intelligence, and decision theory. All these areas deal with complex problems that can be made more clear by carefully considering the limitations that determine the structure of the problem.

This article shows how constraint processing can be used to solve optimization problems in multi-agent systems (MAS). Distributed approaches to optimization problems with constraints (DCOP — distributed constraint optimization) are considered. In DCOP, a set of agents must come to some kind of agreement (usually through some form of discussions) about what actions each agent should take to jointly get the best solution for the entire system [1]. This structure has been successfully used not only for planning meetings, but also in sensor networks, where the sensors must agree on what purpose they should focus on in order to get the most accurate assessment of the location of the goals. To test the effectiveness of DCOP decision algorithms, tasks of checking the feasibility of Boolean functions and graph coloring are often used. A common key aspect of DCOP for MAS is that each agent only negotiates locally with a subset of other agents (commonly called neighbors) that can directly affect its behavior. Depending on the formulation of the problem and the solution methodology used, this aspect can significantly reduce the computational effort faced by each agent, which makes complex problems accessible even for large-scale systems. So in the meeting planning task, the agent will directly negotiate only with those agents with whom he should meet, which usually is a small subset of the agents involved in the whole problem.

Along with multi-agent approaches, metaheuristic optimization methods are being actively developed, which although they do not guarantee finding the exact solution, they usually allow finding an acceptable solution in an acceptable time [2]. A possible DCOP formalization for a meeting planning task includes a set of agents representing the people participating in the meeting, and a set of variables that represent the possible start time of the meeting according to the participant. Constraints prescribe equality for variables representing the start time of the same meeting of different agents, and ensure that variables that represent the start time of different meetings of the same agent do not match. Finally, preferences can be presented as soft constraints on the start time of meetings, and the overall goal is to optimize the sum of all soft constraints. Although we have personal preferences in this parameter, we maximize the sum of the preferences of all agents, and thus, we consider the scenario when the agents fully cooperate, that is, they are ready to reduce their own local utility if it maximizes global utility [3].

2. Materials and methods

A key element for distributed constraint processing is the concept of a network of constraints. We give standard formal definitions related to constraint networks, and then consider the very paradigm of distributed constraint processing.

The network of constraints N is formally defined as a tuple <X, D, C>, where X = {x₁, …, x_n} — is a set of discrete variables, D = {D₁, …, D_n} — is the set of variable domains that list all possible values of the corresponding variables, and C = {C₁, ···, C_m} is a set of constraints. The C_i limit can be of two types: hard or soft.

Constraints can be defined for any subset of variables, however, the most visual work in constraint networks (both decision algorithms and theoretical analysis) is shown on binary constraint networks, where each constraint (soft or hard) is defined by two variables.

A distributed solution involves using a set of agents that monitor variables and interact to find a solution to a network of constraints.

Formally, DCOP can be represented as a network N = <X, D, C>, containing soft restrictions, plus a set of agents A = {A₁, A₂, …, A_k }. Finding the best DCOP solution is an NP-hard problem. Therefore, the empirical evaluation of DCOP solution methods is a crucial point in assessing their possible practical application [4-5].

Given the previous description of DCOP, we consider the exact solution methods, that is, those that always find the solution that corresponds to the best value of the objective function (global optimum). These methods are especially interesting and elegant from a theoretical point of view, but since we are dealing with the problem of NP-completeness, they also exhibit exponentially increasing coordination costs (either in the size, or the number of messages exchanged, or in the calculations performed by each agent) , the number of agents in the system is increasing.

In general, approaches can be divided into two classes: those that are based on search [6-10], and those that use dynamic programming [11]. In addition, search-based approaches are divided into synchronous, such as SyncBB [10] and AND / OR search [9], and asynchronous, such as ADOPT [6], NCBB [7], and AFB [8]. In the synchronous execution model, agents wait for messages from other agents before they compute and send new messages themselves. In contrast, in the asynchronous model, agents perform calculations and send messages without waiting for messages from their neighbors. An asynchronous operation is desirable in a multi-agent approach, as it allows agents to make decisions without waiting for other agents to complete their calculations, making full use of parallel computing. On the other hand, the synchronous model ensures that agents always have the most up-to-date information before performing calculations, thus minimizing redundancy in both calculations and communication.

All of the above methods are completely decentralized, in the sense that each agent has full control over its variables and knows only about relevant restrictions. However, centralizing part of the problem can sometimes reduce the effort needed to find the best global solution. This concept is the basis of the Optimal Asynchronous Partial Overlay (optAPO) approach [12]. The optAPO algorithm seeks to detect parts of the problem that are particularly difficult to solve in a decentralized way (parts that are highly interconnected) and centralize them into subtasks that are delegated to intermediary agents that act as centralized solvers). Practice has shown that optAPO consistently reduces communication overhead compared to other decentralized methods such as ADOPT. However, it is very difficult to predict which part of the task will be solved centrally, and therefore it is difficult to predict the costs of computing resources that intermediary agents will spend.

To solve this problem, we used the pyDCOP package — this is a DCOP solver written in Python [13], which has the following features:

• provides implementations of many classic DCOP algorithms;
• allows you to easily implement your own DCOP algorithms, providing all the necessary infrastructure: agents, messaging system, collection of metrics;
• simplifies the conduct of distributed experiments, since agents can work on the same computer or on different computers;
• provides multi-platform, as it can work on Windows, Mac and Linux;
• suitable for use on the Internet of Things (IoT) and can run agents on single-board computers, such as the Raspberry Pi.

The task of creating the schedule was successfully solved in Python and posted on the portal of decision-making support web services ws-dss.com (see Fig. 1).

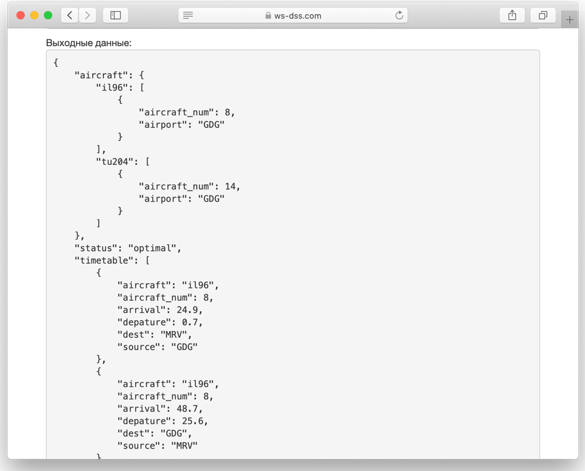
Figure 1

Several works using ADOPT try to reduce the computation time. For example, in [14], the BnB-ADOPT method was proposed, which is an extension of ADOPT; it successively reduces the computation time using various search strategies: the depth search and the branch and bound method. In [15], the use of preprocessing methods to search for ADOPT was proposed and it was shown that this can lead to a significant increase in productivity.

3. Results and Discussion

The ADOPT approach is proposed — an effective multi-agent method for solving practically important applied problems. The software product created on the basis of the results obtained in this work was tested on the task of creating schedules. Memory usage by each agent is polynomial in the number of variables, which is a significant advantage of this approach compared to dynamic programming. In addition, all messages have a fixed size. However, the number of messages that agents must exchange is, in the worst case, exponentially in the number of variables. This affects the time required to find the best solution. In particular, the number of message synchronization cycles is determined by the number of all agents that received incoming messages and sent outgoing messages, and is exponential. Such exponential elements are inevitable in finding the exact optimal solution and can seriously limit the dimension of the problems being solved.

MAS can minimize the number of information agents who should disclose information to each other (thus increasing the level of confidentiality). This is because, in DCOP, agents need to know only about the limitations in which they are involved.

In general, the DCOP structure and the algorithms developed to solve such problems represent an active area of research in the MAS community, which is increasingly being applied in real conditions.