High water and floods on rivers caused by snowmelt and rain fall are a characteristic feature of the river regime. Runoff during the flood period, flood height, and rain flood height are the elements whose forecasts are particularly important. To develop methods for forecasting these regime elements, it is necessary to know the general patterns of formation of melt and rain runoff in river basins.

Any river basin can be considered as a kind of dynamic system, which generally reflects the genesis of runoff in the basin [1]. It is affected by the processes of water supply to the surface of the basin from melting snow or rain, the processes of retention and loss of incoming water by the basin, and the processes of excess water draining into the channel network and along it to the closing gate.

A characteristic feature of the processes listed above is their large unevenness in space (in area) and in time. This is due both to the very nature of some of them (for example, uneven precipitation) and to the heterogeneity of the river basins themselves, their topography, soil and vegetation cover, and the depth of ground water. Each of the processes depends on a larger or smaller number of factors, some of which cannot be directly measured. But even those that can be measured are measured with far insufficient detail. All this leads to the fact that a quantitative (mathematical) description of each of the processes of runoff formation in a river basin is possible only in a schematized or averaged form [2].

All factors that determine the formation of runoff in a river basin are divided into two categories: constant physical and geographical and variable hydrometeorological. The former include the size, configuration of the basin, its geological structure, topography and associated density and pattern of the hydrographic network, surface and channel slopes, soil and vegetation cover, lake area and wetlands of the basin. Variable factors are atmospheric precipitation, its quantity and intensity, heat influx, which determines the intensity of snowmelt and evaporation, water absorption capacity of the soil, which in turn is determined by its nature and previous humidity, and for meltwater-the depth of freezing and soil temperature. These factors ultimately determine the variability of the above-mentioned runoff elements.

Water supply. By this term we mean the amount of water entering the surface of the pool per unit of time (from rain or snowmelt), expressed in millimeters per hour or millimeters per day.

Total feedrate. The total amount of water that reached the pool surface during rain or snowmelt, expressed in millimeters.

Water output. Pool water recovery. The amount of water released by the pool to runoff per unit of time and expressed in millimeters per hour or in millimeters per day. In other words, the pool water output is the difference between the water supply and its absorption per unit of time.

Reaching the water. This term, applied to a swimming pool, refers to the regular sequence with which the flowing water passes through the closing gate.

In general terms, the water output of the basin u is expressed by a simple water balance equation [3]

y = h — p

(1)

where h is the water supply; p is the pool’s water absorption and evaporation losses.

A similar equation can be written for the runoff for the entire period of a rain flood or flood

Y = X — P

(2)

where Y is the runoff minus ground supply; X is the total water supply; P is the total amount of water absorbed and lost by the pool, which is often referred to as runoff losses.

In the above equations, only Y and X are measured values and can be estimated with varying degrees of accuracy. The supply value h for the case of rain can also be measured. As for runoff losses, they cannot be directly measured and practically only their total value can be approximately determined from the water balance equation as the difference between the total water supply and runoff [4]

P = X — Y

(3)

It follows that the main task of calculating the water recovery of the basin, and therefore of predicting runoff, is to determine the amount of water retained and lost by the basin or runoff losses. Let us therefore consider in more detail what they consist of.

The main reasons that not all the water coming to the surface of the pool flows into the river are: 1) its absorption into the soil and 2) its retention on the surface of the basin in various kinds of depressions, such as large non-capillary pores between clumps of soil in its upper layer, various negative microrelief shapes and entire catchments of lowlands or drainless lakes and ponds. Surface retention also includes water costs for wetting vegetation cover when rain falls. The third element of runoff losses is evaporation from the catchment area surface during the period of rain or snowmelt, as well as after the end of supply from the surface of draining water.

Before getting into the riverbed network, flowing rainwater or meltwater must fill all the pockets of surface detention, where it remains in the form of numerous puddles, and in addition, in drainless swamps, lakes and artificial ponds. In the absence of water absorption into the soil, filling of surface retention foci occurs directly as the total water supply increases. In the presence of soaking, filling of these pockets can only occur due to the excess water supply above the seepage. The total amount of water retained by the pool consists of the amount of water absorbed into the soil and retained on the surface of the pool. The water retained on the surface of the pool is further absorbed into the soil, and part of it evaporates.

Surface retention depends on the nature of the river basin. All other things being equal, it is larger in pools with flat terrain and smaller in pools with well-dissected terrain. It also depends on the type of soil and its structure, which determine the moisture capacity of its loose upper horizon, and on the nature of agricultural land cultivation [5]. This factor is estimated for each region and basin in advance and, to some approximation, it can be taken into account as a constant when preparing predictive products.

Rain flood forecasts based on precipitation data are one of the most difficult tasks in practice. Its difficulties are mainly related to the large unevenness of the processes of rain runoff formation and the lack of data that would allow us to take this unevenness into account [6].

There are quite a large number of methods for calculating the hydrograph of rain floods, which can be used for short-term forecasts of water flows and levels. All of them are based on the principle of summation of simultaneously reaching water masses and differ from each other only in the methods of calculating the water recovery of the pool and determining the functions of reaching the runoff. According to the first feature, all known calculation methods can be divided into three groups:

methods based on the use of empirical dependences of rain runoff on precipitation and water absorption factors;

methods based on the use of data on the inflow of water into the river network of the basin, calculated from hydrometric data;

mathematical models for calculating floods based on precipitation с using electronic computers.

As for the methods for determining the runoff, runoff functions, they can also be divided into three groups, which are discussed below.

There are three ways to determine the runoff reach functions:

1. by constructing an isochron map.

by defining a single hydrograph.

by analytical means, based on assumptions about the nature of the regulatory action of river basins and the selection of parameters of the accepted reach function in relation to this basin.

The isochron method. The essence of this most ancient method is that the distribution of areas enclosed between isochrons of water reaching is taken as a function of runoff reach. The simplest way to construct a map of isochrons in a river basin is based on the assumption that the speed of reaching is constant and is reduced to drawing isolines on the basin map connecting points equidistant from the closing gate. Having determined the isochron of the area enclosed between them from the map, divide them by the entire area of the pool and get the distribution of relative areas of simultaneous water flow.

The disadvantage of the runoff reach function obtained in the described way is that it does not sufficiently reflect the regulatory effect of the river basin. The hydrograph calculated using this run-up function needs to be transformed later. The calculated hydrograph is taken as an inflow to a hypothetical reservoir that acts like a lake or reservoir. To transform the inflow hydrograph, it is necessary to have a volume curve or use the assumption thatthere is a linear relationship between volume and flow and choose a time constant at which the best convergence of the transformed hydrographs with the actual hydrographs is achieved. In this case, the use of the isochron method was proposed by A.V. Ogievsky [2].

A single hydrograph. The definition of a single hydrograph is reduced to three simple operations:

allocation of underground runoff on the flood hydrograph;

determination of the surface runoff layer for a flood;

division of flood costs (net of ground feed) by the surface runoff layer.

Determining a single hydrograph from a single flood may not be reliable enough. Therefore, it is necessary to identify several such hydrographs by selecting a number of floods caused by rains of the same duration. The duration of precipitation is taken as the duration of the most intense (runoff-forming) part of the rain (Fig. 1), and even better, water recovery.

The average unit hydrograph for a basin is determined by averaging several hydrographs obtained for the same duration of precipitation or water output [7].

When determining individual hydrographs, it is best to select isolated floods caused by relatively uniform short-term rains over the territory and over time.

As an approximate characteristic of the basin’s inherent runoff distribution, a single hydrograph better reflects the regulatory role of the basin than the distribution of interisochronous areas. However, when determining it, a number of difficulties arise, the main one of which is that the unevenness of precipitation over the territory and over time has a significant impact on the form of flooding. And since the nature of rain is very diverse, the determination of individual hydrographs only on the basis of the duration of precipitation in many cases is insufficient.

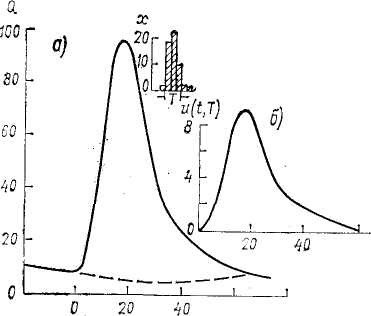
Flood hydrograph (where a is a unit hydrograph; b is for a given precipitation duration T)

Calculation of the flood hydrograph, if a single hydrograph is known for a given duration of water loss, is performed by multiplying its ordinates by the total water loss layer [7]:

Qi = YU(t,T)

(4)

where Y is the total water recovery layer, mm; U (t, T) is the symbolic designation of the ordinates of a single hydrograph as a function of time and duration of water recovery.

As we can see from the information provided, for an adequate operational determination of the probability of flooding, regardless of the forecast method used, we need to have a high-quality and rain-measuring network. Otherwise, based on (4), a strong smoothing of the desired values will be observed. Currently, there are more than 3.6 thousand weather stations in the Russian Federation, and in total there are more than 12 thousand different observation points in the network. At the same time, as the head of Roshydromet notes, «in 2005-2010, the validity of storm warnings was at the level of 89-91%, now it is already 95-96%. That is, it is sufficient both in advance and in completeness of information so that local authorities can take preventive measures»[8].