- Introduction.
The Federal State Educational Standard of Primary General Education [5 ] contains provisions according to which it is necessary to develop in primary education the skills of schoolchildren associated with planning their own actions in accordance with the set task and the conditions for its implementation.
It should be noted that the ability to plan one’s actions is associated with the ability to act «in the mind», which underlies the development in the mental, internal plane of a method for obtaining the expected result in these specific conditions.
It can be said that in the mind (i.e. with images of things, and not with the real things themselves) a person has to act when he must know in advance the result of his activity and the method of obtaining it in accordance with the set goal. Acting “in the mind”, «to himself», in the internal (mental) plane, a person operates not only with visual (or schematic) images of things, but also with their designations, in particular, words of natural language.
Thus, various kinds of mental reasoning, reflections, dialogues often occur without the participation of visual images, objects and events. An example of this can be, in particular, an oral (or in terms of internal speech) solution to such a logical problem: “Three years ago, Konstantin was two years younger than Grigory will be in a year. Who is older and by how much?”
According to the provisions of developmental psychology [ 2 ], the ability to act “in the mind” develops most intensively precisely at primary school age, since the basic skills of educational activity are formed during this period.
Characterizing the new mental qualities that appear in children at this time, V.V. Davydov writes: “The more “steps” of his actions a child can foresee and the more carefully he can compare their different options, the more successfully he will control the actual solution of the problem. The need for control and self-control in educational activities, as well as a number of its other features (for example, the requirement for a verbal report, assessment) create favorable conditions for the formation of the ability of primary school children to plan and perform actions to themselves, in the internal plane” [1; 83].
In relation to the age under discussion, the development of the ability to act internally (or, what is the same, the development of the internal plan of action) was most thoroughly studied by Ya. A. Ponomarev [4].
To study the features of the internal plan of action, he developed a special task scheme. First, the child was taught some simple objective action (for example, a separate move of some chess piece), and then he was offered problems where he had to independently construct a sequence of these actions (from the moves of this chess piece — a knight, rook, bishop, etc. — in order to capture a pawn).
In some cases, when solving such problems, the child was allowed to look at the playing (chess) field with the pieces placed on it, and in other cases, the name of the squares of the field, their location and the initial arrangement of the pieces were asked to remember and solve the problem, mentally imagining the field and the movements of these pieces on it.
In the most general sense, it was considered that the children who can solve problems with a large number of moves and without looking at the playing field have an internal plan of action formed at a higher level than children who are not able to solve problems without relying on visual aids.
- Materials and methods.
To determine the stage of development of the internal plan of action of younger schoolchildren studying in the first, second, third or fourth grade of primary school, you can use the tasks proposed by Ya.A. Ponomarev. These tasks are designed for individual work with a student within 20-30 minutes.
In contrast, we developed the task «Knight’s Jumps», which is intended for group, frontal work with a class of students [3 ].
When developing this task, we used problems that involve a solution related to moving an imaginary chess knight in the required number of moves.
Completing such a task included two parts. The first of them required mastering various movements of the knight in one move. In the second part of this task, it was proposed to solve problems in which it was necessary to construct a system of knight’s moves,
It is necessary to note an important difference between the task we developed and the task used by Ya.A. Ponomarev in individual experiments.
The fact is that when solving problems in the conditions of group experiments, it was proposed to mentally move an imaginary knight along a visually given nine-cell playing field.
And when solving problems on moving a knight in the conditions of individual experiments, it was required to mentally move the knight along an imaginary nine-cell playing field.
A diagnostic lesson on the material of the task «Knight’s Jumps» with a class of younger schoolchildren was conducted as follows.
At the beginning, the organizer of the diagnostic lesson (psychologist or teacher) draws on the board (60×60 cm) so that its cells are clearly visible to the students from the last desk. Three vertical rows of cells are designated by letters (A, B, C) at the bottom of the field, and three horizontal rows are designated by numbers (1, 2, 3) at the side of the field, for example:
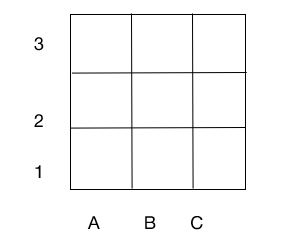
Fig. Playing field.
The diagnostic lesson is held in the form of a game.
Having drawn the playing field, the organizer explains: “To play on this nine-cell square, you need to know how its cells are designated. Each cell has a name that consists of a letter and a number. For example, the corner cell on the left in the lower part of the square is called A1, and next to it, on the same line — B1, in the middle of the field — B2”.
Then he suggests practicing naming the cells.
After the organizer is sure that almost all the students have learned the designation of the squares, he explains the move of the chess knight — the rules for its movement on the square field.
«The knight does not jump along adjacent squares, but through one square. But even through one square, it jumps not just along one line (for example, from A1 to A3 or from A1 to C1) and not just from one corner square to another corner (for example, from A1 to C3 or from A3 to C1). It jumps through one square so that one of the squares must be a corner, and the other non-corner (for example, from A1 to B3 or from C2 to A3)».
During training in the correct moves of the chess knight, the organizer names the starting square (from which the knight jumps), and the students — the ending square (which the knight gets to in one jump) and. on the contrary, the organizer names the final cell (which the knight gets to in one jump), and the students name the initial cell (from which the knight jumps).
Since the diagnostic lesson should take one lesson, then, as our experience has shown (especially in working with first-graders), there is no need to try to teach the chess knight move right there in the classroom to those children who do not have time to master it right away. We have to put up with the fact that a small part of the children do not have time to master the chess knight move, and move on to the next stage of diagnostics.
Further, the organizer of the lesson talks about the possibility of coming up with many problems, knowing the move of the chess knight and the rule for its movement: “The simplest problems consist of two knight moves. For example, first the knight stood in cell A1 (this is the initial cell), then jumped to an unknown cell, and from this cell jumped to cell A3 (this is the final cell).
In the conditions of such problems, unknown cells are indicated by a question mark, and jumps are indicated by straight lines between the names of cells, for example: A1 — ? – A3.
In a two-move problem, you need to guess the unknown intermediate cell where the knight was after the first move and from where it can get to the final cell with the second move. In this problem, such a cell can only be cell C2.
Using the move of the chess knight, you can come up with not only two-move problems, but also three-move and four-move problems, for example, A1–?–?–A2 or A1 –? – ? –? –C3.
The answer to a two-move problem is written as follows: No. 2. B1 (the problem number and the name of the intermediate unknown cell are indicated), to a three-move problem – as follows: No. 5. B3; C1, to a four-move problem – as follows: No. 10. B3, C1, A2″.
After this, the organizer gives each student a sheet of 12 problems, for example:
- A1–? –A3.
- A2 –? – B3.
- A3 –? – C3.
- B3 –? – C2.
- C3 –? – ? – C2.
- C2 –? – ? – C1.
- C1 –? – ? – B1.
- B1 –? – ? – A1.
- A1 –? – ? – ? – C3.
- A2 –? – ? – ? – C2.
- A3 –? – ? – ? – C1.
- B3 –? – ? – ? – B1.
Drawing the children’s attention to the content of the problems they have received, he explains that problems one through four are solved in two moves. In the answer to these problems, on a blank sheet of paper where you have indicated your last name, you need to write the name of one cell; problems five through eight are solved in three moves, in the answer to them you need to write the names of two unknown cells; problems ninth through twelfth are solved in four moves — in the answer to them you need to write the names of three unknown cells.
You need to solve the problems in a row, looking only at the cell field drawn on the board. Any other auxiliary fields (drawn on the desk, pieces of paper, on your hands, etc.) cannot be used.»
The meaning of the requirement to solve problems looking only at the playing field placed on the blackboard is clear: if a child has a field in front of him (for example, on a desk), which he can touch with his hand or pencil, then solving the problem is significantly easier, since it is possible to calculate the options and plan the solution not «in his mind», but on paper with a pencil.
If a child needs to solve problems looking at a field that cannot be touched, then he is forced to do all the necessary calculations and preliminary fittings mentally, «in his mind», in the internal plane.
It is worth noting the following technical point: a class of students should be offered not one version of the problem, but two or, best of all, four. To do this, it is enough to vary only the initial cells in the problems.
For example, in relation to the above version of the series of problems, it looks like this:
- A2 – ? – B3.
- A3 – ? – C3.
- B3 – ? – B2 etc.
The third option can be constructed in the same way in relation to the second option, as the second option was constructed in relation to the first (i.e. making the second task the first, the third task the second, etc.).
The more options for the 12 tasks assignment there are in the class, the more reliably it will be possible to establish the level of formation of the internal action plan for each student in the class.
When determining the level of formation of the internal action plan, it is advisable to focus on the following provisions.
If a child can name the final cell of a knight’s jump given the initial cell is known, or name the initial cell of a knight’s jump given the final cell is known, then this characterizes the manifestation of the first level of formation of the internal action plan.
If he cannot name the final or initial cell given the initial or final cell is known, then this characterizes the manifestation of the zero level of formation of the internal action plan.
If a child can correctly solve two-move problems, this characterizes the manifestation of the second level of formation of the internal action plan.
If a child can correctly solve not only two-move problems, but also three-move problems, this characterizes the manifestation of, respectively, the third level of formation of the internal action plan.
If a child can correctly solve not only two-move and three-move problems, but also four-move problems, this characterizes the manifestation of, respectively, the fourth level of formation of the internal action plan.
- Results.
Using the material of the task «Knight’s jumps», which proposes to solve twelve problems of three levels of complexity (two-move, three-move and four-move), at the end of the school year, group experiments were conducted with schoolchildren of the first, second and third grades.
The results of solving problems by students of the noted classes in group experiments are presented in the table.
Table. The number of students of the first, second and third grades who correctly solved four two-move problems, four three-move problems and four four-move problems.
|
Class
|
Number of students
|
Problems |
|
Two-move Three-move Four-move |
||
|
1
2
3 |
36
32
34 |
10 (27,8%)** 4 (11,1%) 0 (0,0%)
14 (43,8%) 7 (21,9%) 3 (9,4%)
21 (61,8%)** 11 (32,3%) 7 (20,6%) |
| Note: *p< 0.01.
|
||
The data presented in the table allow us to note the following.
The number of children correctly solving two-move problems increases most intensively from class to class.
Thus, in the second grade, in relation to the first, the number of such children increased by 16.0%, and in the third grade, in relation to the second, there were 18.0% more of them. It should be noted that the difference in the indicators related to the first and third grades, respectively: 27.8% and 61.8%, is statistically significant (at p < 0.01).
The number of children correctly solving three-move problems increases less intensively from the first grade to the third grade, respectively: 11.1%, 21.9% and 32.3%, and the number of children correctly solving four-move problems, respectively: 0.0%, 9.4% and 20.6%.
Characterizing the development of the internal action plan in primary school students who took part in this study, it is necessary to note the following.
Firstly, among first-graders there are no children whose internal action plan is formed at the fourth level, since not a single child solved all four-move problems correctly.
In contrast, such children are in the second and third grades, respectively: 9.4% and 20.6%.
Secondly, in each class the number of children with the second level of formation of the internal plan of action (i.e. children who correctly solved four two-move problems) is greater than the total number of children with the third and fourth levels of formation of the internal plan of action (i.e. correctly solving, respectively, four three-move and four four-move problems).
In general, the data obtained in group experiments with first, second and third grade students solving twelve problems of the «Knight’s Jumps» method allowed us to characterize the features of the distribution of levels of formation of the internal plan of action among students in incomplete primary school.
- Conclusion.
The conducted study was aimed at determining the level of formation of the internal action plan of primary school students studying in the first, second and third grades of primary school. A diagnostic task «Knight’s Jumps» was developed, designed to conduct frontal diagnostics in the form of a group experiment with a class of students. A total of 102 primary school students participated in the study: 36 first-graders, 32 second-graders, 34 third-graders.
Conducting a diagnostic lesson on the material of twelve tasks of the task «Knight’s Jumps» made it possible to determine the quantitative characteristics of the formation of the internal action plan of first-graders, second-graders and third-graders.
For the first time, it was established that the number of first-graders, second-graders and third-graders who have the second level of formation of the internal action plan exceeds the total number of peers who have the third and fourth levels of formation of the internal action plan.
Knowledge of this fact expands and clarifies the ideas of age and educational psychology about the features of the formation of the internal plan in primary school and about the characteristics of the development of intellectual activity of younger students in general.
In the future, it is planned to conduct research on the material of twelve tasks of the «Knight’s Jumps» method in order to determine the level of formation of the internal plan of action in fourth-graders, as well as in fifth-graders and sixth-graders.
This will allow us to obtain data characterizing the distribution of the
levels of formation of the internal plan of action among students of each noted age.
The data of the noted studies are of serious practical importance, since they can be used to improve the education of schoolchildren of nine-ten and eleven-twelve years old.
References
1. Davydov V.V. Mental development in primary school age. – In the book: Age and educational psychology / Ed. A.V. Petrovsky. Moscow, 1973. 288 p.2. Davydov V.V. Lectures on educational psychology. – Moscow: Academy, 2006. 222 p.
3. Zak A.Z. Thinking of a younger student. - St. Petersburg: Assistance, 2004. 828 p.
4. Ponomarev Ya.A. Knowledge, thinking and mental development. – Moscow, 1967, 264 p.
5. Federal state educational standard of primary general education / Bulletin of Education of Russia. – 2010. – No. 2. – P.10 - 38.
