1.Introduction.
One of the important problems of modern education, in particular primary education, is the development in children of the ability to think logically correctly, reason consistently, and draw a consistent conclusion from the proposed judgments [5]. Solving this problem is necessary to achieve an optimal level of preparation of children in order to increase the effectiveness of education in secondary school.
It is known that the curriculum of middle and high schools is rich in scientific concepts and patterns in academic subjects of the natural sciences (mathematics, physics, biology, chemistry) and the humanities (literature, history, social studies).
The purpose of the present study was an experimental study of the conditions for solving problems of a logical nature in the fourth grade.
To achieve this goal, two cycles of experiments were carried out. The 1st cycle was associated with solving logical problems, where it was necessary to find the missing elements of classes (sets) [3], in the second cycle they were asked to solve problems related to determining an unknown class (set) based on indirect signs [4].
- Materials and methods.
2.1. First cycle
The purpose of this cycle of research was to study the capabilities of children in achieving results in problems associated with “searching for the missing elements of a set.” 48 subjects took part in the first (preliminary) and second (main) series of the first cycle. In the preliminary series, the goal was to determine the characteristics of children obtaining correct and incorrect results when searching for missing elements of classes (sets). The main series of experiments was aimed at determining how correct and incorrect answers when solving the noted problems are related to the level in which the required result is achieved (subject or figurative).
2.1.1. The first (preliminary) series of experiments.
The following task was used as the experimental methodology in this series:
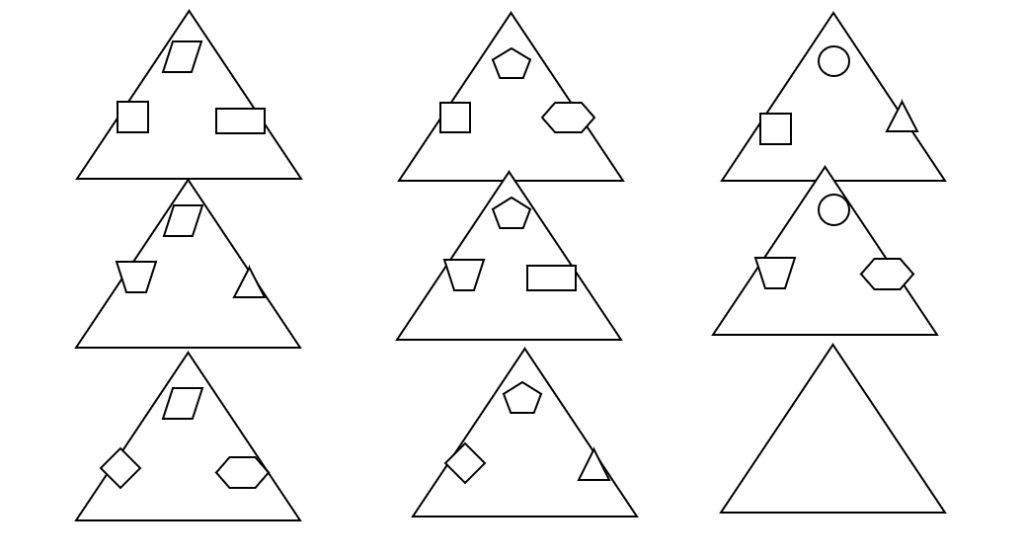
Fig 1. Condition of the problem of the first series of experiments
The student was told: “The artist drew nine large triangles and images in them. There are no images in the ninth triangle. Do you need to know what images and how to place them in the ninth triangle?”
The structure of this task can be represented in a sign model as follows:

In this model, the letters of the Russian alphabet (A, Б, Г) designate small figures located in the left corner of each large triangle, numbers (1, 2, 3) — figures located in its upper corner, letters of the Latin alphabet (Q, W, Z) – figures located in the right corner.
1 series was related to solving the above problem.
It was necessary to find out the features of correct and incorrect approaches to finding the correct result in problems associated with “searching for missing class elements.”
As a result of the experiments, it turned out that some children successfully coped with this logical problem (group 1), while other children were unable to cope with this problem (group 2) — see Table 1.
The students included in the first group were characterized by carrying out quick inspection of small geometric shapes located in the corners of eight large triangles. As a result, these children immediately assumed that there was a missing circle in the upper corner of the empty triangle.
However, after this they carefully examined the eight drawings proposed in the task conditions in order, as they said, “…to find out what might be suitable for placement at the bottom of the ninth triangle…”.
Observing the actions of these subjects, it was possible to notice that they understood how the small figures were placed on the left side inside the large figure: “… in each row it is the same…” and indicated that a rhombus should be drawn in the empty large triangle.
After that, they looked at the remaining eight triangles for a long time. It was clear from their actions — some children even used their fingers to hold the two hexagons in images 2 and 6, or the two small triangles in images 4 and 8 — that they wanted to find out how the small shapes in the right corner of the triangles were distributed.
As a result, some children came to the conclusion that “…in each row there are three different ones…” and therefore in an empty large figure you need to draw a rectangle.
Other children — namely those who touched the drawings with their hands — discovered the rule by which small figures are distributed on the right side of large figures, and also said that “… a rectangle is needed here…”.
The children who made up the second group of subjects in this series acted differently. The first part of this group, as a rule, did not carefully look at all the small figures found in the eight large figures. For them, it was sufficient to examine three images, including image 9, either in the same horizontal row (specifically, images 7 and 8) or in the same vertical row (specifically, images 3 and 6).
At first they believed that large figures should have a pentagon and a triangle at the top and right, and a rhombus on the left. They justified this assumption as follows: on the right, in the lower part of the large figure, small images will be repeated, because in images seven and eight the rhombus is repeated.
Then, also based on the idea of repeatability of figures, they proposed to draw a circle in the upper corner, a trapezoid in the left, and a hexagon in the right. This means that they were, in fact, proposing to fill triangle 9 with the same shapes that were in triangle 6.
The second part of the children in this group examined all the triangles and usually came to the conclusion that a circle should be placed in the upper corner of triangle 9.
Some children suggested drawing a rectangle in the lower corners of the rhombus figure, based on the repeatability of the rhombus in triangles 7 and 8, while others suggested drawing a rhombus from triangles 7 and 8 in the left corner of triangle 9, and a hexagon from triangle 6 in the right corner.
An analysis of the actions of the subjects of both parts of the second group shows that they were unable to discover the principle of placing small figures in the right corner of the triangles.
Comparing their behavior in the process of achieving the result with the subjects of the first group, it should be noted that the children who successfully solved the problem (first group) took into account the location of the small figure in the triangles, and also sought to understand the principle of placing the figures in the corners of all eight triangles. And only after understanding it did they conclude what small figure would be in the corresponding corner of triangle 9.
Students who did not cope with this logical problem sought to immediately find out what should be placed in the triangle 9 in the upper corner, left and right. Therefore, noticing the repeatability of some figures, they assumed what and how should be placed in triangle 9.
Behavior of children in group A shows that they acted indirectly, analyzing the relationships of elements in the content of the problem in order to highlight the essential relationships of these elements.
Such actions indicate that they used a theoretical method of action to achieve a result.
The children of group B did not conduct such an analysis and relied only on a simple comparison of the elements of the conditions to find a solution. In this case, we can say that an empirical (direct) method of action takes place (for more details on the characteristics of the theoretical and empirical methods, see, for example, [1], [2], [3], [4]).
2.1.2. Second (main) series
The purpose of the experiments was to clarify the nature of the connection between the method of solving logical problems of the type under consideration and the organization of problem solving: when in one case, children’s actions are performed in terms of perception of the conditions of the problems (i.e., in a visual plan), and in the other case, in an objective-action plan, in materialized form.
36 students who solved the problem “with triangles” unsuccessfully, at the experimenter’s suggestion, solved another logical problem of the same type, which, although there were visual differences, was constructed in the same way as the logical problem where it was necessary to compare triangles.
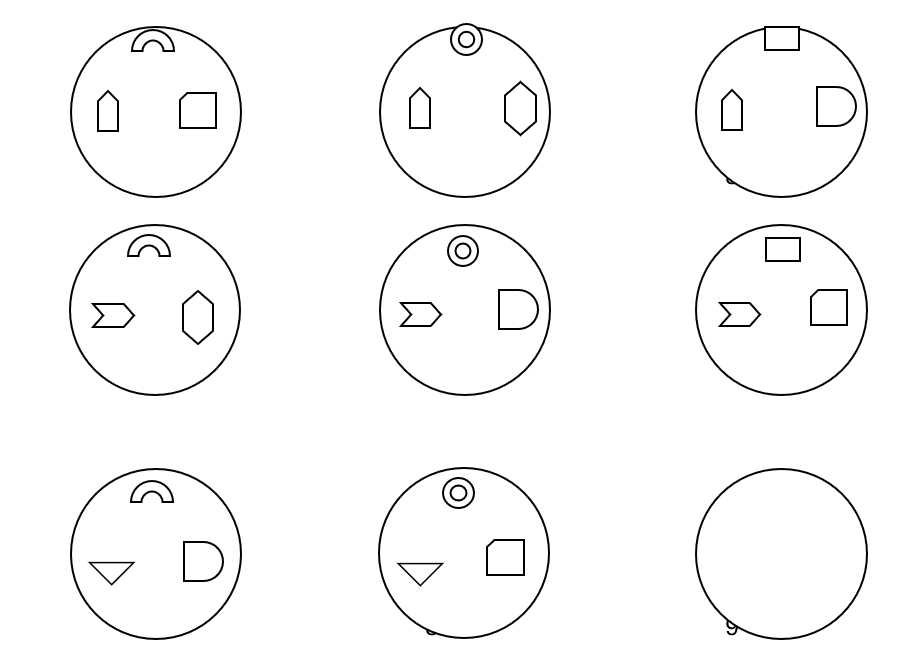
Fig. 2. Logical problem for series 2
In the second problem, three classes of 9 elements of three types were used: images at the top of the circle, at the bottom of the circle and in the center on the right.
To analyze the second problem, the same model representation of elements of the three classes as for the first problem is suitable.
The second series of experiments was carried out as follows. 36 schoolchildren who failed the first problem were divided into three parts in this series: B.1, B.2 and B.3.
One part of the schoolchildren was asked to look for the result of a new task in terms of perceiving the drawings in its conditions (i.e., in a visual way).
The subjects of group B.2 again dealt with triangles. Children were asked to first copy the contents of eight pictures by sequentially tracing large triangles and small figures within them. It was necessary to act sequentially: circle triangle 1 and three small figures in it, then triangle 2 (and three small figures in it), then triangles 3 — 8 (with small figures in them). After this, it was proposed to determine what should be placed in triangle 9.
Children from B.3 were again presented with the first problem. It was necessary to first copy the contents of the eight images by sequentially drawing large triangles (and small figures in them) onto another sheet, and then begin to achieve the required result. The formation of the three marked groups was carried out in order to determine the influence of the conditions for carrying out search actions on achieving the required result.
On the one hand, it was necessary to find out the possibilities when searching for the result of actions carried out in a visual way. On the other hand, it seemed necessary to clarify the possibilities of materialized actions consisting of tracing and drawing images that make up one or another class of objects.
The main experiments showed the following: a minority of group B.1. found the correct answer to the second problem, acting in a theoretical way, i.e. highlighting the important relationships between the elements of the second logical problem that determine the correct solution.
The majority of children in this group, when solving the second logical problem, also acted unsuccessfully, using, similar to the behavior when solving the first logical problem, an unproductive approach, which is associated with a direct search for suitable figures based on a direct comparison of the depicted elements.
After this, these children were asked to circle the pictures in the condition of this task.
As a result, it turned out that after tracing the lines, all the children coped with the first logical problem, since they discovered the repeatability of small figures in three large figures, firstly, vertically (triangles first, fourth, seventh; second, fifth, eighth; third, sixth ninth), secondly, horizontally (triangles first, second, third; fourth, fifth, sixth; seventh, eighth, ninth), thirdly, in different places in three rows (triangles first, sixth, eighth; second , fourth, ninth; third, fifth, seventh).
All subjects of groups B.2 and B.3 correctly identified the composition of small figures in triangle 9 after copying the images.
With regard to the actions of schoolchildren who make up B.2, we can say that some children of this group identified a “horizontal” pattern of distribution of images in triangles based on the content of the first row — 1, 2 and 3, and other children — on the basis of the content of the second row, – 4, 5 and 6.
Moreover, all children in this group discovered a “vertical” pattern in the distribution of images based on the content of the second row.
Children from group B.3 also acted differently when copying images. The majority of children discovered “horizontal” repeatability of figures after copying the images of the first row, and a minority — based on the content of the 2nd row.
“Vertical” repeatability of the distribution of images for children of subgroup B.3.1. discovered after based on the content of the 2nd row, and children of subgroup B.3.2. – after copying all images.
In general, the completed series showed: changing the conditions for carrying out search actions when achieving the required result in relation to the missing elements of the class contributed to the transition of many children from an unsuccessful, direct approach in obtaining the required result to a successful, indirect approach — theoretical (see Table 1).
2.2. Second cycle of experiments
The purpose of the experiments in this cycle was to study the solution to a logical problem related to the search and selection of a given class of objects. A preliminary (first) series and a main (second) series were conducted.
In the preliminary series, it was necessary to determine the characteristics of children’s actions leading to correct and incorrect answers. In the main series, it was necessary to find out how the actions to achieve the correct and incorrect answer are related to the conditions under which the decision is made: in a visual sense (i.e. in terms of perception of the proposed combinations of signs) or in a substantive sense (i.e. in materialized form — copying combinations of characters).
Fifty-six fourth grade students participated in both series in April and May.
2.2.1. Preliminary series
In this series of experiments, it was proposed to solve different versions of the following problem:

Each child was given a sheet on which the condition of this task was depicted: eight combinations of four signs. In each combination, the characters occupied different positions: the first position — on the left edge, the second position — on the left in the middle, the third position — on the right in the middle, the fourth position — from the right edge.
At each of these positions there was a sign of a certain type: the first position was occupied by any unvoiced letter, the second by any number that is divisible by two, the third by any vowel letter, the fourth by any number that is not divisible by two. This distribution of signs allows you to conceive a different number of them: 1, 2 or 3.
First of all, the student was asked to consider 8 complexes and each of them had 4 signs. Then the experimenter said that the child could point to any of the eight combinations or complexes of signs on the playing field and guess some two or three positions in it. The child needed to find out what was in these positions. For this purpose, he could indicate one or another complex of four positions where, in his opinion, there are the necessary signs.
If the chosen combination contained all the guessed positions, then the child was informed of the correct guess. If this combination did not contain everything that the experimenter had guessed (for example, two positions out of 3, or one position out of 2 guessed, or there were none of the required positions), the child was informed that his the answer is incorrect.
For example, first the experimenter (psychologist) thought of F, 2, 5 in combination (2) — F 2 E 5. Then he informed the child that in combination (1) some three signs were thought of. The child could then point, for example, to the combination (4) – F 2 A 3 and ask: “In this combination, out of four characters, are there three hidden ones?” The psychologist had to say: “Absent.”
Then the student had the opportunity to name the combination (2), – F 2 E 5. With this option, the psychologist should have said “Yes.” In this case, the subject could say: “The signs F, 2, 5 were hidden.” The psychologist then reported that the decision was correct.
Based on the material of the 8 complexes presented above, the child had to cope with the problem associated with finding two hidden signs (these were signs E, 5): “In combination 3, two signs were hidden. Guess these signs.»
This series was associated with clarifying the specifics of solving the proposed problems based on empirical and theoretical approaches.
The experiments showed that a minority of schoolchildren who took part in this cycle of experiments (group A) solved the proposed problem successfully (i.e., in the least number of choices, usually four or five), and the majority of children (group B) either guessed the required signs using a large number of extra choices (more than 10), or could not guess them at all (see Table 2).
The subjects of group A acted as follows. Yes, still without offering any complex of signs, these subjects carefully examined all eight complexes in order to find out where the complexes containing the positions that were in the sample were located (M 2 E 5).
As a result, they discovered (as could be judged by their remarks and pencil movements between combinations of characters) that combinations with the letter M were in the left column, and with the number 2, the letter E and the number 5 were in both columns. At the same time, they also noted that the number 2 does not change, but the letters A and E, numbers 3 and 5 alternate.
After this, the subjects of group A sequentially checked their guesses about pairs of hidden signs. In this case, different strategies were used.
Some children acted like this. First they pointed to combination 1, asking: “Is combination 1 suitable?” If this was incorrect, then the children said, for example: “… that means it’s not M-2…”.
Then they asked: “Is combination 7 correct?” If this was also incorrect, they said, for example: “…that means it’s not M-E…and not 2-E…”.
Next they asked: “Is there 5 in the combination?” After the experimenter answered “No,” they said, for example: “… that means it’s not M-5 and not 2-5…”.
This choice prompted two schoolchildren to answer: “Signs E, 5,” and two more schoolchildren made a new attempt: “Is there 2 in complex?” When the psychologist answered positively, the schoolchildren proposed a solution: “These are signs E, 5.”
Some children in this group acted differently. They, firstly, pointed to the combination 5 and, after a negative answer from the experimenter, noted: “… this means it’s not M-2, not M-5, not 2-5…”. Secondly, they pointed to the combination 7 and after the experimenter answered “No”, they said: “… that means it’s not M-E and not 2-E…” and then offered a solution: “… E, 5 …».
Two schoolchildren, in contrast to the actions of the marked subjects, chose combinations differently. First of all, they chose combination 7, and when it turned out that this was incorrect, they concluded: “… this means it’s not M-2, not M-E, not 2-E…”.
Then they pointed to combination 5 and, taking into account the psychologist’s negative answer, concluded: “… not M-5 and not 2-5, … but … E-5.”
The observed behavior of schoolchildren in group A allows us to assert that they perform two types of analysis: analysis of the distribution of combinations with identical signs, and analysis of the result of verification of assumptions about the presence of the required signs in a particular complex.
Group B subjects solved the problem differently. Unlike the subjects of group A, they did not carry out either an analysis of the distribution of combinations or an analysis of combinations of characters in twos — they acted randomly.
For example, at first they pointed to combination 1 and after the experimenter’s negative answer they did not draw any conclusions, but simply pointed to another combination — combination (5). Having received a negative answer, they again did not comprehend the current situation in any way and pointed to combination 7.
After a negative answer, most children refused to solve the problem further, stating: “I can’t guess…” or “I don’t know how to proceed…”.
The other part of the subjects continued the solution. These children further pointed to combination 2 and, after an affirmative answer from the experimenter, named at random one of three possible pairs of signs: 2-5, 2-E or E-5.
When asked why this or that pair of signs is the answer, they usually answered that “… these signs are both here and there…” or “… they are in combinations of 3 and 2… » The fact that they still needed to prove their answer and that not every pair of characters from combination 2 was suitable for an answer was not taken into account by them.
Comparing the actions of test groups A and B, we can say that in group A there was an indirect approach to achieving the required result, associated with analyzing the features of the distribution of complexes in the content of the problem, putting forward hypotheses before the next choice and understanding its result.
Other schoolchildren (B) took a direct, empirical approach to achieving the required result, since they did not analyze the results of the moves performed, and when they correctly guessed the desired complex, they directly compared it with the original combination.
As one could find out in a conversation after the experiment, many subjects acted like this: they tried to name combinations one after another with the expectation that in the end a combination would be chosen that might contain the one they were looking for, and then in this combination they would choose some two positions.
2.2.2. Second (main) series of experiments
This series involved 44 people who solved problems empirically (Group B). These children had to cope with the second logical problem, which was constructed in the same way as the first, with the only difference being that the original combination was F 2 А 3, in which two signs A, 3 were also guessed.
This problem could be optimally solved in two choices, for example, the first choice is combination 8 (checking such pairs of characters as F-2, F-A and 2-A), the second choice is combination 6 (checking such pairs of characters as F -3, 2-3). After this, it was possible to name the solution — signs A-3.
In the second series, the subjects of subgroup B.2 solved the proposed problem in the same way as in the first series — using the signs of the presented combinations in a visual-figurative manner.
Subgroup B.1 subjects were asked to act differently: they first had to write down the presented combinations of characters on another sheet (in this case they had to write down the combinations in a row in accordance with the numbers: 1, 2, …, 7, 8), and then they were asked solve the second problem (i.e. the one where the original combination was 4).
As a result of the experiments of the second series, it turned out that none of the children of subgroup B.2 acted in an optimal way when solving the problem, that is, they did not put forward or test hypotheses about pairs of hidden signs.
Among the subjects who copied combinations, there were children who were able to switch to the optimal method of action, and those children who did not change their method of solving the problem.
As can be seen, the actions of the children who were able to move to the optimal method, when they copied different combinations of signs, indicated that they paid attention to the repeatability of the signs in the copied combination in relation to the previous one.
Thus, they noted that in combination 2 there is the same figure with combination 1, in combination 3 there are the same three characters with combination 2, etc. And after completing their copying work, they considered all eight combinations, noting the repetition of characters in the columns.
Answering the question about the symbols that needed to be found in the fourth complex, the schoolchildren controlled the search actions: they named the next complex not just to see what would happen, but in order to check the presence of certain signs in it.
During the copying process, some children were not interested in the relationships between characters in combinations, simply trying to copy without errors. Further, already in search of an answer, they acted at random, similar to their actions in the preliminary series.
The second series showed: a change from a visual plan to an objective-action one (i.e., from the actions of perceiving combinations of signs to copying them) contributed to the transition of a number of children from an empirical, direct approach in searching for a result to a theoretical, indirect approach associated with analyzing the content of the proposed task (see table 2).
- Results.
Quantitative characteristics of children’s success in solving problems in the first and second cycles of individual experiments are reflected in the first and second tables.
3.1. Results of the experiments of the first cycle
Table 1
The number of subjects who successfully solved the problem of the first cycle in the first and second series in a visual and actionable manner (in %).
|
Series |
Problem Solving | |
| Successful | Unsuccessful | |
| Action form | ||
| Visual — subject- figurative effective | Visual — subject- figurative effective | |
|
1 series
2 series |
25,0 –
8,3 69,5 |
75,0 –
22,2 – |
The results posted in the first table reflect the following features of achieving results in logical problems of the first cycle of the study.
In the first series, 75.0% of schoolchildren solved the problem “to find the missing elements of a set” in a visual sense (when perceiving the conditions of this task) unsuccessfully; significantly fewer children, respectively, 25.0%, managed to achieve the required result.
In the second series, it was shown that only 8.3% of children (of those noted in the first series, 75.0%) were able to successfully solve a new problem of the same type in a visual way. At the same time, 22.2% of the children out of the noted 75.0% failed to cope with the new logical problem in a visual sense (when perceiving its conditions).
It was also shown that a significant part of the children — 69.5% (of those noted in the first series of 75.0%) coped with the new logical problem in an objectively active, materialized way (by tracing and copying the presented images of figures).
In general, in the first cycle it turned out that a change in the organization of achieving the required result when solving the logical problem of this cycle (search for missing elements of classes), associated with the implementation of search actions in the materialized plan, significantly contributes to obtaining the correct result.
3.2. Results of the second cycle of research
Table 2
The number of subjects who coped with the logical problem of the second cycle in the first and second series in visual and objective-action plans (in%).
|
Series |
Problem Solving | |
| Successful | Unsuccessful | |
| Action form | ||
| Visual — subject- figurative effective | Visual — subject- figurative effective | |
|
1 series
2 series |
21,4 –
— 36,4 |
78,6 –
36,4 27,2 |
ZThe results posted in the second table reflect a number of features of achieving results in logical problems of the second cycle of the study.
In the first series, the overwhelming majority of schoolchildren (78.6%) unsuccessfully solved the problem “to find a given class of objects” in a visual way, and significantly fewer schoolchildren — 21.4% — coped with the logical problem in a visual way.
In the second series, it was shown: 36.4% of children were unable to successfully solve a similar problem visually, and the same number of children (36.4%) coped with this problem visually.
In addition, another 27.3% of children coped with this problem in a subject-based manner. To achieve the required result, they were asked to copy eight combinations of characters onto another sheet.
In general, in the first cycle it turned out that a change in the organization of achieving the required result of the logical problem of this cycle (search for missing elements of classes), associated with the implementation of search actions in the materialized plan, significantly contributes to the achievement of the correct result.
So, as a result of both series of the second cycle confirmed the results of the first cycle. It was again shown that changing the organization of achieving the required result of the proposed problem, associated with the implementation of search actions in the materialized plan, significantly contributes to obtaining the correct result.
- Conclusion.
In the above series of experiments with fourth grade students, methods were used based on the material of problems where it was necessary to find the missing elements of sets and determine an unknown class (set) based on indirect signs.
In each cycle there were two experimental series — the first, preliminary, and the second, main.
In the preliminary phase, it was necessary to find out the possibilities of schoolchildren’s search actions when achieving the required result in the proposed problems. In particular, it was necessary to establish whether children could cope with these problems when carrying out actions in a visual way, i.e. in terms of perception of either pictures in the problems proposed in the first cycle, or combinations of signs in the problems proposed in the second cycle.
The meaning of the main series was related to finding out what role the conditions for carrying out search actions play in the child’s achievement of the required result — in a visual plan or in an objective-active plan.
To do this, a number of schoolchildren who were unable to solve the problem visually in the preliminary series were asked to re-solve a similar logical problem also visually.
Other schoolchildren, who also did not perform successfully in the preliminary series, were asked to act in an objective-action plan: either by tracing the pictures, or by copying combinations of signs.
So, two cycles of research in which fourth-grade students took part give reason to conclude the following: changing the conditions for achieving the required result when posing logical problems, associated with replacing a visual plan with a subject-based plan, creates positive opportunities for children of this age to cope with such problems where it is required to find the missing elements of a set and determine the unknown class (of sets) by indirect signs.
References
1. Zak A.Z. Development of theoretical thinking of junior schoolchildren. M.: Pedagogika, 1984. 241 p.2. Zak A.Z. Diagnosis of theoretical thinking in younger schoolchildren // Psychological Science and Education. – 1997. – No. 2. – P.36 – 41.
. Zak A.Z. Thinking of a primary school student. St. Petersburg: Assistance, 2004. 828 p.
4. Zak A.Z. Diagnosis of differences in the thinking of younger schoolchildren. M.: Genesis, 2007. 159 p.
5. Federal state educational standard for primary general education [Electronic resource] // Federal state educational standards. M.: Institute for Strategic Studies in Education RAO. URL: http://standart.edu.ru/catalog.aspx?CatalogId=959 (access date: 09/04/2024).
