Поскольку плодородные земельные участки являются ограниченным ресурсом, то качество их использования является одной из характеристик развития АПК. С этой точки зрения урожайность посевных культур, её динамику можно рассматривать как способ определения эффективности хозяйственного ведения в сельскохозяйственной отрасли. С другой стороны, постоянно увеличивающиеся потребности в качественных продуктах питания требуют мер, направленных на увеличение урожайности культур, чтобы при неизменных посевных площадях получать большее количество урожая.

Поэтому целью работы является исследование динамики изменения урожайности масличных культур, а также построение моделей, описывающих это изменение.

В качестве объекта исследования выступают временные ряды изменения средней урожайности масличных культур, к которым относятся подсолнечник, соя, горчица, рапс озимый и рапс яровой, за период с 1990 г. по 2015 г [1].

Проводя первичный анализ с использованием описательных статистик [2, с. 482], можно отметить, что средняя урожайность масличных культур составляет 10,9 ц/га. При этом среди исследуемых культур наибольшую урожайность имеют рапс озимый и подсолнечник (у_ср=15,8 ц/га и у_ср=11,4 ц/га соответственно), наименьшую – горчица (у_ср=5,33 ц/га).

Проверим с помощью критерия Фостера-Стюарта наличие тенденции в исследуемом ряду [3, с. 109].

Каждый уровень ряда сравним с предыдущим и определяем значения

.

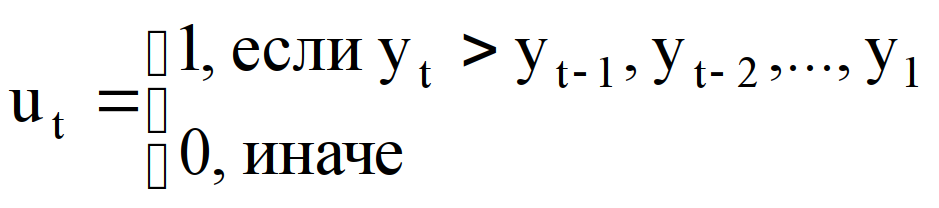
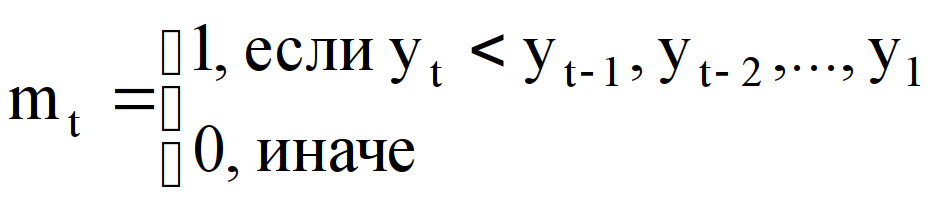Далее вычисляем

и

. Для проверки гипотез о случайном характере величин S—μ и D-0 с помощью критерия Стьюдента определяем расчётные значения критерия:

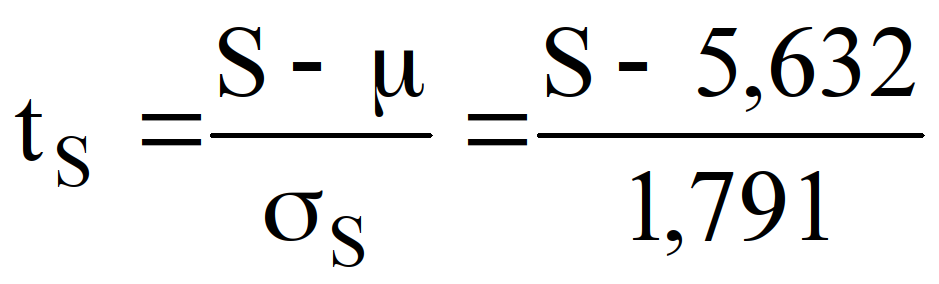и 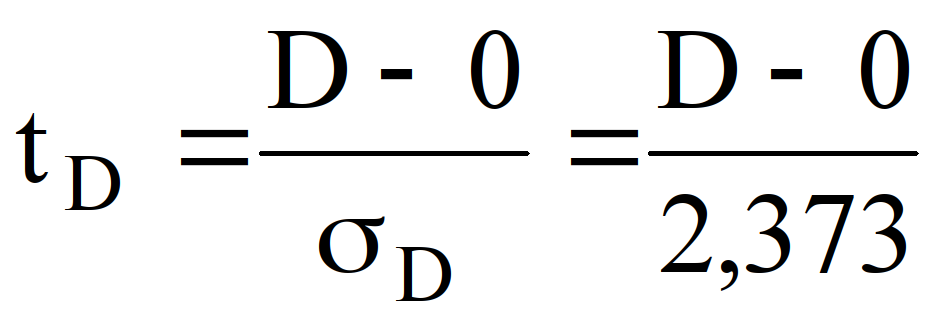, где значения μ – мат. ожидание величины S, σ_S – среднеквадратическая ошибка величины S и σ_D – среднеквадратическая ошибка величины D, находятся из таблиц при n=26 [4, с. 76]. Из таблицы распределения Стьюдента находим критическое значение t_кр=2,0639. Если

, то с вероятностью 95% можно утверждать, что в исследуемом временном ряду существует основная тенденция. Аналогично, если

, то в исследуемом ряду присутствуют периодические колебания. Полученные исследования показали, что во всех случаях есть основная тенденция и отсутствуют периодические колебания.

Проведём анализ для урожайности масличных культур в среднем (рис. 1).

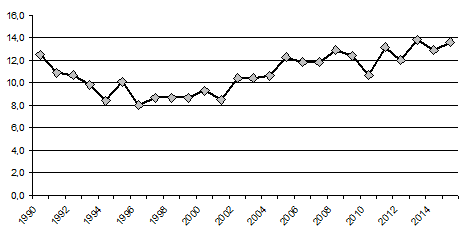
Рисунок 1. Динамика урожайности масличных культур

Для выбора лучшей формы тренда по зерну в целом сравним линейную, квадратичную и показательную регрессии.

Линейный тренд:

, R²=0,431, все параметры значимы по критериям Фишера и Стьюдента [5, с. 62].

Квадратичный тренд:

, R²=0,652, все параметры значимы.

Показательный тренд:

, R²=0,409, все параметры значимы.

Таким образом, в качестве уравнения тренда необходимо выбрать квадратичную функцию. Параметр b₀ здесь показывает начальные условия развития процесса, т.е. средняя урожайность масличных в 1990 в РФ составляла 10,88 ц/га; параметр b₁ – постоянный темп роста, другими словами, с каждым годом урожайность масличных падает на 0,28 ц/га; параметр b₂ – темп прироста, который показывает скорость изменения этого процесса, т.е. с каждым годом скорость падения урожайности масличных культур увеличивается на 0,016 ц/га.

Проверка адекватности моделей реальному процессу проводится на основе анализа случайной компоненты. Принято считать, что модель адекватна, если значения остатков удовлетворяют свойствам случайности, независимости и нормальности распределения.

Предположение о нормальности остатков может быть проверено с помощью показателей асимметрии и эксцесса [6, с. 315]:

,

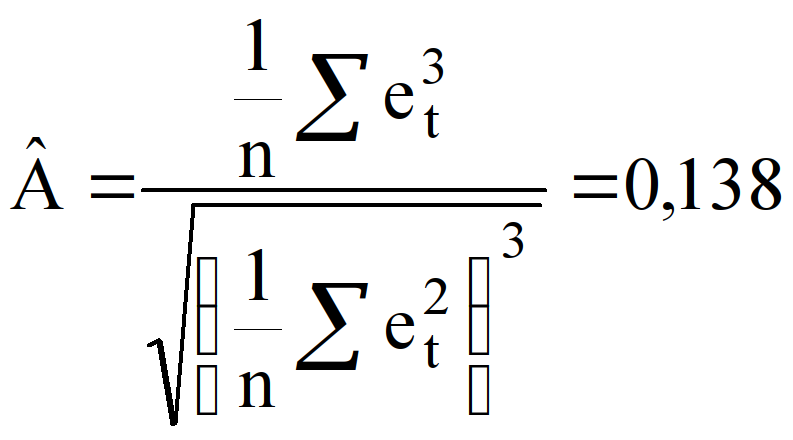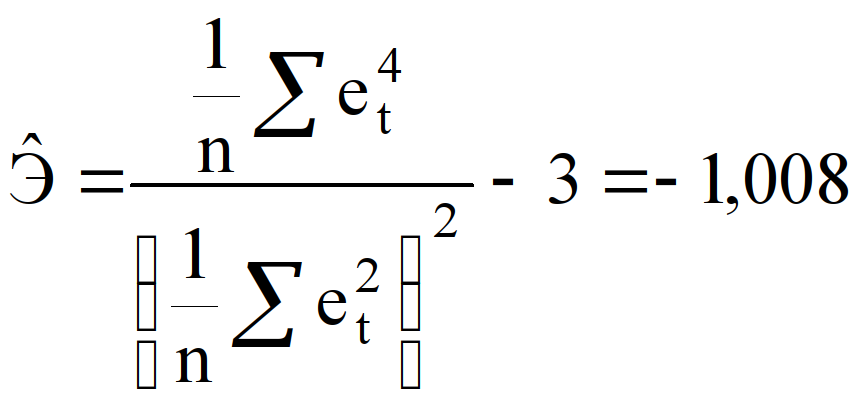
. Среднеквадратическая ошибка асимметрии равна

.

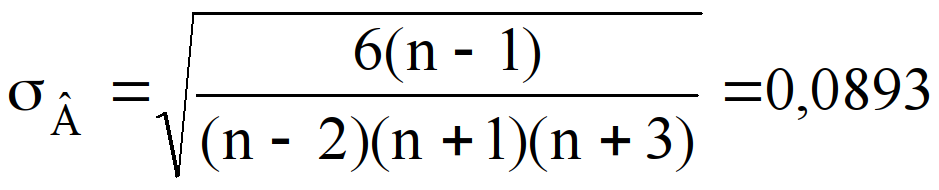Среднеквадратическая ошибка эксцесса –

.

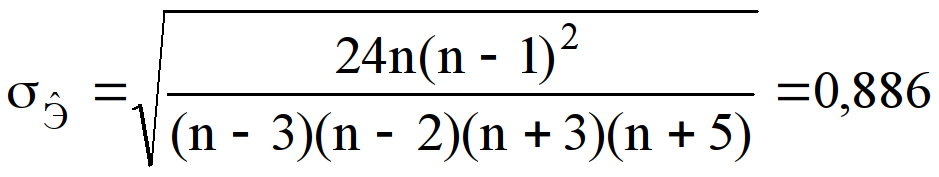Т.к.и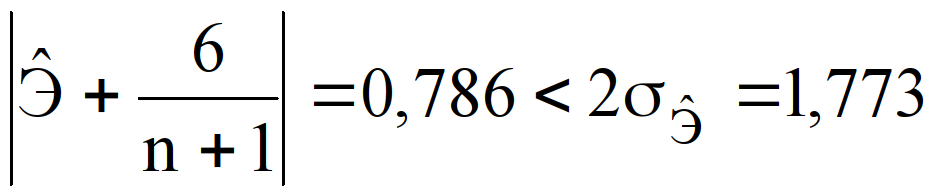

, то гипотеза о нормальном характере распределения принимается.

Независимость остатков можно проверить с помощью критерия Дарбина-Уотсена [7, с. 108]. При уровне значимости 5% и n=67 критические значения Дарбина-Уотсена составляют d_L =1,30 и d_U=1,46, тогда 4-d_U=2,54 и 4-d_L=2,7. Фактическое значение d=1,762, построенное для нашей модели, принадлежит интервалу [d_U, 4-d_U], следовательно, гипотеза о независимости случайных отклонений принимается.

Случайность уровней ряда остатков можно проверить с помощью критерия медианных серий [4].

Число серий для ряда длиной n=26: v(26)=12, протяжённость самой длинной серии kmax(26)=4, тогда

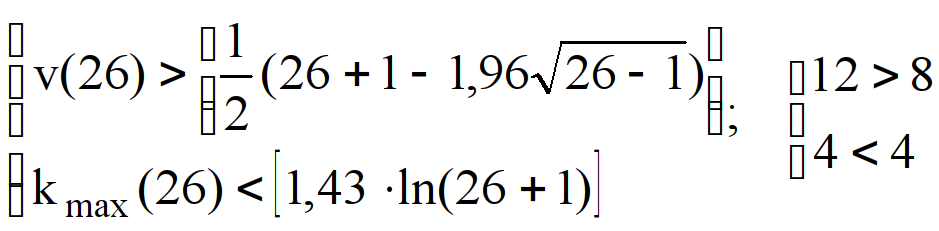. Оба неравенства выполняются, следовательно, гипотеза об отсутствии тенденции среднего уровня принимается, и ряд остатков можно считать случайным.

Другими словами, построенную модель можно использовать для прогнозирования урожайности масличных культур в РФ.

Построим прогноз урожайности по выбранной квадратичной модели: у(t=2016)=14,98 ц/га, y(t=2017)=15,59 ц/га. При этом ошибка аппроксимации составляет А=8,56%.

В качестве заключения можно отметить, что проведенный анализ показал в целом рост урожайности масличных культур за последние 26 лет. Однако данный рост характеризуется квадратичным трендом, т.е. до 2003 наблюдалось сокращение урожайности и лишь в период с 2004 по 2015 год наблюдается увеличение урожайности. Падения урожайности всех рассматриваемых культур в 2010 г обусловлены засухой на территории РФ и большим количеством пожаров. Всё это свидетельствует о качественных изменениях в АПК, способствующих рациональному землепользованию и усилению продовольственной безопасности России.