1.Introduction.
In recent years, reflection has become the subject of study in a number of studies. The most active and multifaceted reflection is studied in works devoted to the identification of mechanisms for creative problem solving. In particular, two types of reflection were distinguished — intellectual and personal, each of which is realized in the appropriate forms [6].
In line with this approach, the solution of problems is considered mainly from the productive and procedural side. In other words, the researchers here find out the originality of the operational and procedural characteristics that contribute to the successful solution of problems. The other side of problem solving, the content-cognitive one, attracts the attention of psychologists to a lesser extent.
1.2. Types of cognitive reflection
Because of this, reflection as a person’s consideration of the grounds for his own actions is studied, in our opinion, not concretely enough. We mean the fact that the solution of the problem can be carried out in a generalized and non-generalized way. This is due to the fact that a person uses different reference points when constructing an action, which serve as the basis for the methods of his actions.
In one case, the grounds are such landmarks that determine the success of an action (or task solution) only in given, particular conditions. In another case, the grounds are such landmarks that determine the success of the action in a wide range of different conditions.
Therefore, from our point of view, an indication that, when solving a problem, a person clarified the reasons for his own actions, is not specific enough: it is not clear what reasons, particular or generalized, a person considered when solving a problem. When solving problems, it is expedient to single out two types of reflection based on the content-cognitive basis. If a person, when solving a problem, relies on particular, situational guidelines and considers them the grounds for his action, then such reflection should be considered formal, since although a person is aware of the grounds for his actions, these grounds are single and situational, i.e., according to In essence, these are pseudo-foundations, foundations only in form.
If a person, when solving a problem, relies on generalized, extra-situational guidelines and considers them the basis of his action, then such reflection should be considered meaningful, since such guidelines are a necessary condition for successfully solving externally different, but internally related tasks, i.e. are contained in various particular circumstances.
It should be noted that both formal and substantive reflection is, in fact, the process of correlating a person’s mode of action with the features the conditions under which this action is to be performed. This correlation should carried out internally, «in the mind».
Such a requirement follows from the fact that the noted correlation occurs in relation to the mode of either an accomplished or an action that has not yet occurred. Faced with a task, a person either tries to use the method already known to him (correlation of the present conditions with the previous method), or tries to develop a new method (correlation of the present conditions with the possible method).
1.2. Types of planning
In studies specifically devoted to the internal plan of action, the ability to act «in the mind» [1], planning [5], it was shown that when solving problems, a person mainly uses two types of plans — partial and holistic.
In the first case, a person plans the next steps, or links, of his decision after he has completed the previous ones. In other words, the planning of an action and its execution alternate.
In the second case, subsequent steps are planned before the previous ones are performed, and the previous steps are planned based on the expected content of the subsequent ones. Here, a person plans all the solutions to the problem at once, the entire sequence of operations in the required action. Holistic planning is characterized by a higher level of internal plan of action, a developed ability to act «in the mind.»
Note that such planning in relation to solving the same problems appears in children at a relatively late age, and among peers it takes place in children with more intellectually developed
2.Materials and methods.
On the basis of the stated provisions on the characteristics of the types of reflection and types of planning, an experimental study was undertaken. The subjects were 32 fourth grade students. The purpose of the study was to establish the relationship between the types of reflection and types of planning in solving problems.
The achievement of this goal was mediated by the following hypotheses: 1) if schoolchildren have a holistic planning, it is more likely that they will function when solving problems of meaningful reflection; 2) in the presence of partial planning, it is more likely to function in solving problems of formal reflection; 3) when meaningful reflection is functioning, the presence of holistic planning is more likely; 4) with the functioning of formal reflection, the presence of a partial level of planning is more likely.
The study included two stages: at the first stage, under the conditions of the frontal experiment, the level of the internal action plan formed by schoolchildren was determined, and at the second, also under the conditions of the frontal experiment, the type of reflection that functioned in solving the proposed tasks was determined.
At the first stage of the study, we used the methodology developed by us, which included the tasks of “Game of repetition” [1].
2.1. Experiments to determine the formation of planning
The group session was organized as follows.
- At the beginning of the lesson, students are given blank sheets of paper on which they need to mark the date and last name, and then write down the solution to the problems.
- Before class or while the students are signing the sheets, the psychologist draws playing fields on the blackboard, putting down numbers on the left and letters below (Fig. 1):
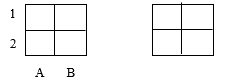
Fig.1. Playing fields
- The names of the cells of the playing field (its notation) are explained to the students: «… the two lower cells are called A1 and B1, and the two upper ones are A2 and B2 …» and their assimilation is checked with the help of appropriate questions.
- The cells of both fields are filled in: in the initial location (on the left) pairs of identical figures are placed, in the final (on the right) — pairs of identical numbers (Fig. 2):
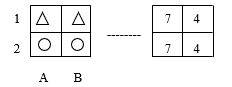
Fig.2. Task condition in one action
- The organizer says: “In this problem, you need to rearrange the figures once so that the same ones are in the same cells. which are the same numbers. To do this, you need to mentally swap some two figures at the same time.
After evaluating the permutation options proposed by the students, the organizer showed on the board on the right side how to write down the solution of problems in one action (Fig. 3).
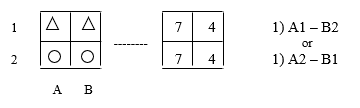
Fig.3. Solving the problem in one action
At the same time, the meaning of the solution found was explained: “… if the circle from A1 is interchanged with the triangle from B2, then the same figures will end up in the same cells where the same numbers are: two triangles will be where there are two sevens, and two circles where there are two fours . Here the solution must be written as follows: A1 — B2. And if a triangle from A2 is interchanged with a circle from B1, then the triangles will be where the fours are, and the circles where the sevens are, and the solution is written as follows: A2 — B1 … «.
- Then the condition of the problem is displayed on the board in two actions (Fig. 4):
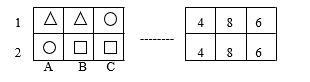
Fig.4. Task condition in two actions
“In this problem, you need to find two actions so that the same figures are in the same cells where the same numbers are.” fter discussing the options for the first and second actions proposed by the children, the organizer wrote down one of the solutions: 1) A1-C1, ) B1-A2 (Fig. 5), explained its meaning: “… first you can swap the circle and square in corner bottom cells, then — a square and a triangle obliquely, diagonally … » and pointed out that » … if there are several solutions to the problem, as in this one, then you need to write only one option …”.
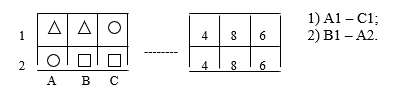
Fig.5. Solving the problem in two actions
- 7. Next, the students were given numbered forms (sheets with the conditions of 20 tasks, — Fig. 6) and were asked to write the number of the form next to the last name on a blank sheet.
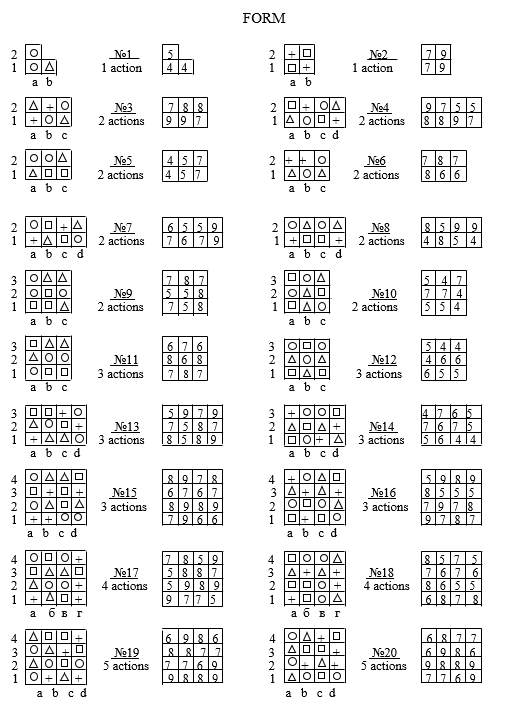
Fig.6. Sheet with conditions 20 tasks
- Then the organizer characterized the location of the tasks on the form: “First, the conditions of the tasks are placed in one action, — No. 1, 2, 3, 4. Then the tasks in two actions — No. 5, 6, 7, 8, 9, 10, in three actions — Nos. 11, 12, 13, 14, 15, 16, in four actions — Nos. 17, 18 and in five actions — Nos. 19 and 20 … «and once again formulated the goal of solving each problem:» … it is necessary for the specified number of actions to place the same figures in the same way as the same numbers are placed … «.
Further, he explained: “Problems solve in a row, starting with the first; you don’t need to copy the conditions of the tasks: on the sheet with the last name, just write the number of the task and next to it, use the names of the cells to write down one, two or three actions, as we did on the board; look for only one solution … «.
After that, he specifically emphasized: “… you can’t make any notes on the form with tasks, as well as on various drafts, pieces of paper, on the table, etc .; tasks need to be solved only mentally, in the mind, and the invented solution should be written down on a sheet with a surname, indicating the number of the task; act carefully and on your own.”
- It should be noted that the introductory part of the lesson (instruction) takes (depending on age) 10-15 minutes, and exactly 30 minutes should be allotted for independent problem solving in order to obtain comparable results for different groups of students.
The correspondence of these tasks to the objectives of the study was that some of them (tasks in two and three actions) could be solved with only a partial level of planning, i.e. the structure of these tasks made it possible to plan each executive action and perform it separately out of touch with the rest. Other tasks (tasks in four and five actions) cannot be solved using this level of planning: it was necessary to outline all the actions as a whole and only after developing a general plan to carry out these actions. These tasks were constructed in such a way that at first glance, different options for the first action seemed correct, but in fact only one option was correct.
2.2. Experiments to determine the type of reflection
At the second stage of the study, we used the previously developed two-part experimental situation [4]. In the first part of this situation, the subject was asked to solve three (four) tasks related to two classes (or two subclasses of the same class) [7]. In the second part, after the successful solution of the problems, it was proposed to group them, to generalize.
If the subject combined tasks on the basis of similarity and external features of their conditions or, conversely, considered all tasks to be different based on differences in these external features, then it was believed that he pointed to the external guidelines of his actions. This was considered as evidence of functioning in solving problems of formal reflection, consideration of the external grounds for one’s action.
If the subject united the tasks on the basis of their belonging to the same class (or subclass), justifying this by the fact that they are solved in the same way, then it was believed that he pointed to the internal guidelines of his action, essential grounds. This was evidence of the functioning of meaningful reflection in solving these problems, consideration of the initial relations that determine the construction of a successful action.
As a specific technique, the technique of «Interchange of letters» was used, which included two training and three main tasks.
Training tasks
- R D W —— W R D (two actions)
- M Y D —— Y D M (two actions)
Main tasks
- P S V K —- S V K P (three actions)
- R M B N —- B R N M (three actions)
- A O U E —- O U E A (three actions)
Opinions
- All main tasks are similar.
- All the main tasks are different.
- The first and second main tasks are similar, but the third is different from them.
- The first and third main tasks are similar, but the second is different from them.
- The second and third main tasks are similar, but the first is different from them.
* * *
The group experiments on the material of this task was carried out as follows.
First, each student in the class was given a sheet with the above task: two training and three main tasks. Here it is necessary to note the following. In reality, many different task options were used in the class, since it was enough to change the consonants in the conditions of the tasks. This allowed students to solve problems more independently.
After the students indicated their names on the sheets, the experimenter on the board explained the rules for moving letters on the material of such a problem situation:
K R S —- R K S
The schoolchildren were told that in this problem they need to move the letters on the left so that they are located like the letters on the right. At the same time, it was explained that for one movement, one move in these problems, a mutual permutation of any two letters is taken. In this problem, you need to swap the letters K and R.
Then the solution of the two-way problem was analyzed:
P M W T —— W T P M
The experimenter explained that in this task it is required to perform two mutual movements of the letters. These movements must be done mentally with the letters located on the left. The arrangement of letters on the left is called the initial, and on the right — the final, required. At the same time, it was pointed out that the meaning of the problem in two moves is that the letters of the initial location, after two mental movements, are in the required location.
Here the experimenter pointed out that, having mentally made the first movement, it is necessary to write down the result obtained, i.e. the arrangement of all letters after one mutual exchange of places. You also need to do after the second mental movement. In general, the solution of the two-way problem is written as follows:
1) P T V M; 2) V T P M.
Then the experimenter showed how the following problem could be solved in two moves:
B M T — T B M
Next, the students were asked to solve the first training problem on the worksheet. The experimenter checked its solution and analyzed the errors, after which he proposed to solve the second training problem, the solution of which was checked again. Only after making sure that the training problems were solved and written down correctly, the experimenter allowed to start solving the main problems.
At the same time, he usually reminded that their solution should be recorded in the same way as the solution of the training ones. The experimenter did not check the main tasks. After their decision, the students were asked to carefully read five opinions about the main tasks, think and write on the back of the sheet the number of that opinion (only one of the five is required) with which the student most agrees. Next to the number of the opinion, it was necessary to briefly explain why the student agrees with this particular opinion, why he considers it the most correct.
Thus, the group experiment consisted in the fact that at first the experimenter on the blackboard explained to the schoolchildren the meaning of the proposed tasks, showed the form for recording their solution, and checked the solution of the training tasks. Then he offered to solve the main tasks and, after solving them, indicated that one opinion out of five should be chosen and briefly substantiated.
It should be said that the three main tasks belong objectively to two subclasses of the same class. The construction and solution of these problems is based on the ratio of places occupied by the same letters in the initial and required positions. This ratio determines such a solution to problems when the movement of one letter must be carried out several times, and the remaining letters — once.
At the same time, the first and third tasks were selected so that they belonged to one subclass of tasks of the specified class, and the second, to another subclass. In the first and third problems, the ratio of the places of letters in both locations was identical: the second, third, and fourth letters (counting from left to right) moved in the initial location of these problems as a result of three actions, respectively, to the first, second, and third places, and the letter occupying the extreme left place, moved as a result of three actions to the extreme right place.
A different relationship between the places of the letters underlay the construction and solution of the second problem. It was built in such a way that the letters that were in the initial position next to each other would, as a result of three movements, not be in neighboring places. And vice versa, the letters that were in the initial location not in neighboring places, as a result of three actions, began to be located side by side.
As a result of solving problems, some children recognized the first opinion as correct, because “everywhere you need to rearrange the letters”, or “in all problems the letters”, or «There are three actions in each task.»
Other children believed that the second opinion was correct, because “there are different letters everywhere.” Several schoolchildren chose the third opinion because “»the third problem has vowels, but the other problems don’t.”
Some of the children chose the fourth opinion, because in “the first and third tasks the letters are rearranged in the same way, but in the second in a different way”, “in the first and third tasks the letters go in a row, and in the second — in different ways”, “… in the first and in the third task, adjacent letters are changed, and in the second — different ones … «.
Children those who chose the first three opinions carried out formal reflection when solving problems, and the children who chose the fourth opinion carried out meaningful reflection.
- Results.
As a result of the experiments, it was found that 40.3% of children carried out holistic planning when solving problems and, accordingly, 59.7% of children — partial planning and that 24.8% of children carried out meaningful reflection and, accordingly, 75.2% of children — formal reflection.
Analysis of the results based on the study of protocols for solving problems by both methods made it possible to establish the following.
Firstly, not all schoolchildren who demonstrated holistic planning when solving the problems of the «Game of repetition» carried out meaningful reflection when solving the problems of the «Interchange of Letters» methodology. Thus, among 40.3% of children with holistic planning, there were 24.8% of children with meaningful reflection and, accordingly, 15.5% with formal reflection.
Secondly, all the schoolchildren who demonstrated partial planning when solving the problems of the “Repetition Game”, 59.7%, then carried out formal reflection.
Thirdly, all schoolchildren who carried out a meaningful reflection — 24.8%, had a holistic level of a formed internal action plan.
Fourthly, a part of schoolchildren who demonstrated holistic planning — 15.%, carried out formal reflection and, accordingly, a part of schoolchildren who carried out formal reflection — 15.5%, demonstrated holistic planning.
Thus, the hypotheses put forward earlier can be considered legitimate.
- Discussion of the results and conclusion.
From the obtained results it follows that the internal plan of action, in particular at the level of holistic planning, is a necessary condition for the functioning of meaningful reflection. But at the same time, it is also an insufficient condition, since, as it turned out, not all schoolchildren who demonstrated holistic planning in solving problems carried out meaningful reflection. The elucidation of the mechanism of this insufficiency, the establishment of additional conditions conducive to the implementation of meaningful reflection, is the task of our further research.
As such additional conditions, the following can be assumed: the form of action when presenting and solving problems, the complexity of tasks, in particular the number of executive actions, the age of the subjects.
In our theoretical [3] and experimental studies [2], we considered the question of the relationship between the form of action in which schoolchildren solve problems and the type of orientation in the conditions of the problem, on the basis of which its solution is deployed. It was shown, on the one hand, that empirical and theoretical types of orientation in the conditions of problems take place when solving problems in different forms of action: object-effective, visual-figurative and verbal-sign.
In other words, regardless of the form of action in which the student needs to solve the problem, he can focus on external, directly perceived features of the conditions of the problem (i.e., orient empirically), or on the internal, essential relationships of its conditions, on generalized guidelines (i.e., act theoretically).
On the other hand, it was also shown that, other things being equal (for example, the age of schoolchildren, the content of curricula, teaching methods), there is a connection between the type of orientation in the conditions of a task and the form of action in which it is proposed to solve it.
It was found that the theoretical approach to solving problems (associated with the allocation of essential relations, generalized landmarks in the conditions of problems) is easier to implement when solving problems in a subject-effective form than when solving them in a visual-figurative and even more verbally — sign form.
It can be assumed that for children who did not find meaningful reflection in the present study, the form of action in which it was proposed to solve problems was too abstract. In other words, the fact that the tasks of the «Interchange of Letters» methodology were proposed to be solved in a visual-figurative form could prevent these children from carrying out meaningful reflection.
In further work with this technique, it will be expedient, if children carry out formal reflection, to offer them to solve the same problems in a more concrete, objectively effective form.
Another condition that can also affect the fact of the implementation of meaningful reflection is, according to our assumption, that depending on the complexity of the task, in particular on the number of executive actions necessary for its successful solution, it is easier or more difficult for a student to single out its conditions are essential relations.
In other words, it is possible that for children who, when solving the problems of «games of repetition», showed a holistic level of planning and, consequently, the ability to mentally cover the entire solution of the problem, all executive actions in general, the tasks of the «mutual permutation of signs» technique had too many executive actions. These tasks were solved by them without highlighting generalized landmarks, which, in turn, prevented the implementation of meaningful reflection.
In further experiments with the «Interchange of letters» method, it is necessary to offer schoolchildren tasks of varying degrees of complexity, in particular, in terms of the number of executive actions, in order to find a level where it will be feasible for them to highlight significant relationships in the conditions of tasks.
The third assumption is that it is generally characteristic for fourth-graders that the integral level of planning executive actions in solving problems has not yet acquired the character of a general ability — such a mental formation that functions in solving various problems. To test this assumption in further research, it will be necessary to conduct experiments with schoolchildren of other ages.
References
1. Zak A.Z. Development of the ability to act “in the mind” among schoolchildren of grades I–X. Questions of Psychology. 1983. No 1. P. 47–62 [in Russian].2. Zak A.Z. (1984). The development of theoretical thinking in younger students. M., Pedagogy [in Russian].
3. Zak A.Z. Typology of the dynamics of the thought process // Questions of Psychology. 1986. No 5. P.72– 84 [in Russian].
4. Zak A.Z. (2010). Development and diagnostics of thinking of teenagers and high school students. M.: Obninsk – SOTSIN [in Russian].
5. Isaev E.I. Planning as a central component of theoretical thinking // Psychological science and education. 2010. Vol. 2. No 4. P. 34–41 [in Russian].
6. Semenov I.N. Research directions of innovative psychology of reflection in the higher school of economics // Psychology. Journal of the Higher School of Economics. 2012. Vol. 9. No 3. P. 37–57 [in Russian].
